glados.no/courses/tfe4146/summary/summary.md

layout	title	description	math	permalink	date
lecture	Oppsumering av TFE4146	Oppsummering av faget TFE4146 høsten 2020.	true	/:path	2020-11-20

{% include toc.html %}

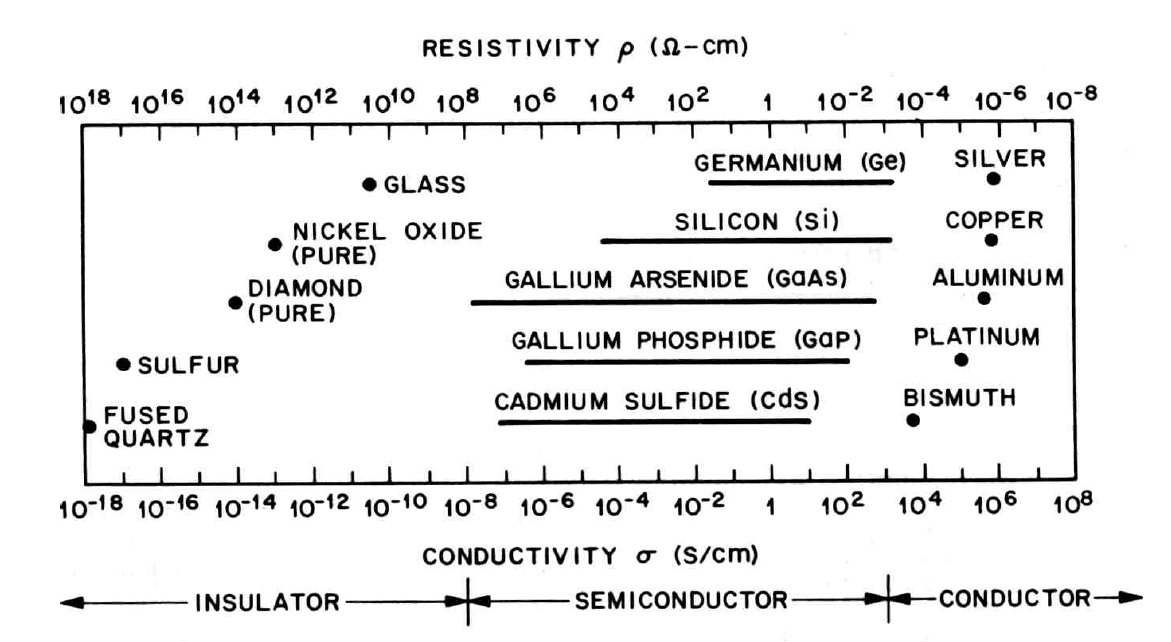
Grunnleggende om halvledere

Historie

• 1830 - Mekanisk
• 1944 - Elektromekanisk
• 1946 - Releer og radiorør
• 1948 - Transistor
• 1958 - Første IC
• 1971 - Første mikroprosessor
• 2020 - Der i er i dag med nanoelektronikk

Moores lov forutser hvor mange transistorer det er plass til per areal. Skal dobles hver 18-24 måneder.

Halvledere

Atomer og elektroner

Uskarphetsrelasjonen

 \Delta x \cdot \delta p_x \geq \frac{\hbar}{2} 

Paulti prinsippet

To like fermioner kan ikke ha den samme kvantetilstanden.

Schrödingers likning

 - \frac{\hbar ^2}{2m}\frac{\partial^2 \Psi(x,t)}{\partial x^2} + V(x)\Psi(x,t) = -\frac{\hbar}{j}\frac{\hbar ^2}{2m}\frac{\partial \Psi(x,t)}{\partial t} 

Løsninger

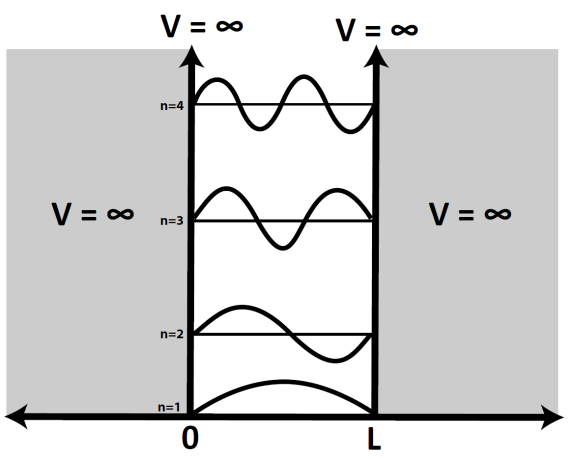
 \psi(x) = Ae^{\pm ikx} \quad E= \frac{\hbar^2 k^2}{2m}

Partikkel i en "boks".

Effektiv masse

 m^* = \frac{\hbar ^2}{\frac{d^2 E}{d k^2}} 

Ser på krumningen til energien i k-rommet. Høy kromming er liten effektiv masse, og vica versa.

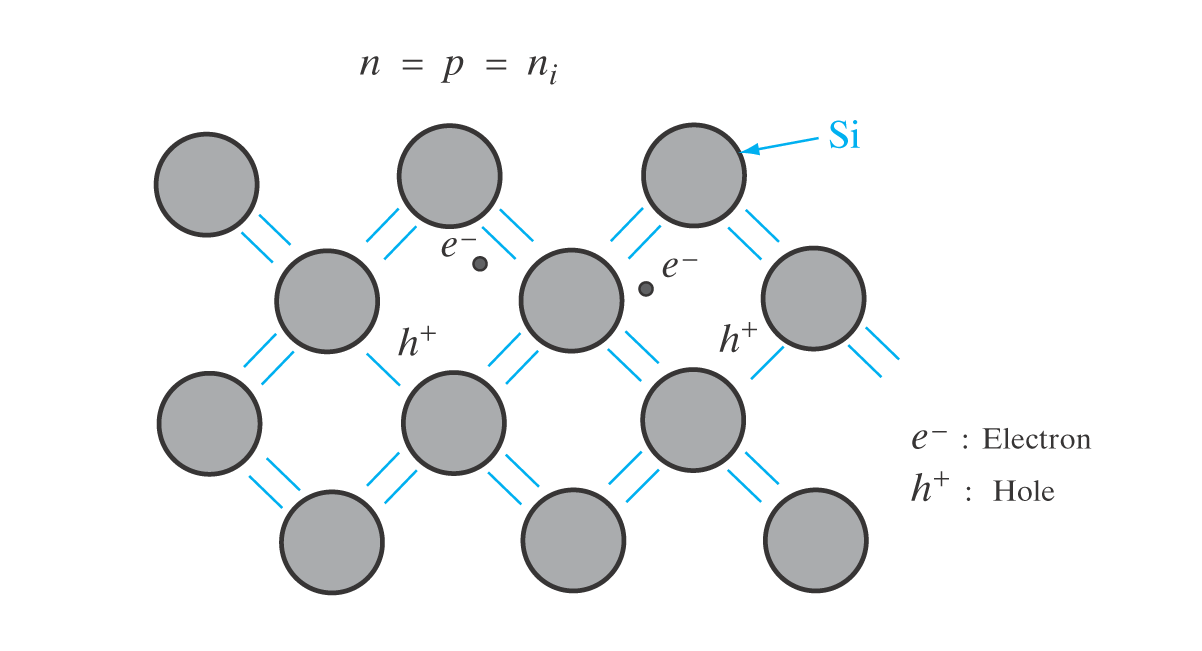
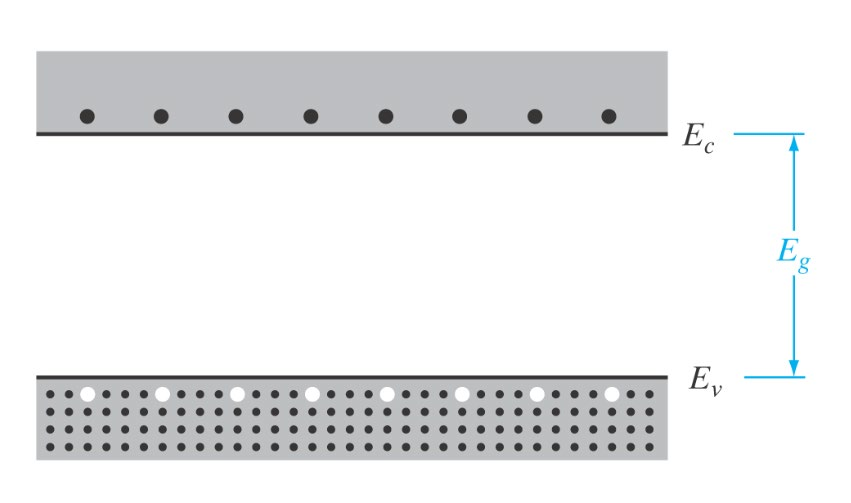
Intrisisk materiale

Inneholder bare en type materiale.

 n = p = n_i 

Der n er tettheten av frie elektroner i lednignsbånd (CB), målt i \text{cm}^{-3}. p er tettheten av hull i valensbåndet (VB), målt i \text{cm}^{-3}. Og n_i er den intrisiske elektrontettheten, målt i \text{cm}^{-3}.

Ekstrinsiske materialer

Disse er intrinsiske materialer som er dopet med et donor eller akseptor materiale.

I Si er det typisk As (Arsenik, donor), eller B (Bor, akseptor).

n-type

 n_0 \gg p_0,n_i 

Der n_0 er elektrontettheten i termisk likevekt.

p-type

 p_0 \gg n_0,n_i 

Der n_0 er elektrontettheten i termisk likevekt.

Elektron-Hull-par i intrinsiske materialer

Elektroner og hull genereres og rekominerer kontinuerlig.

 r_i = g_i 

 r_i = \alpha n_0 p_0 = \alpha n_i^2 = g_i 

Bærertetthet

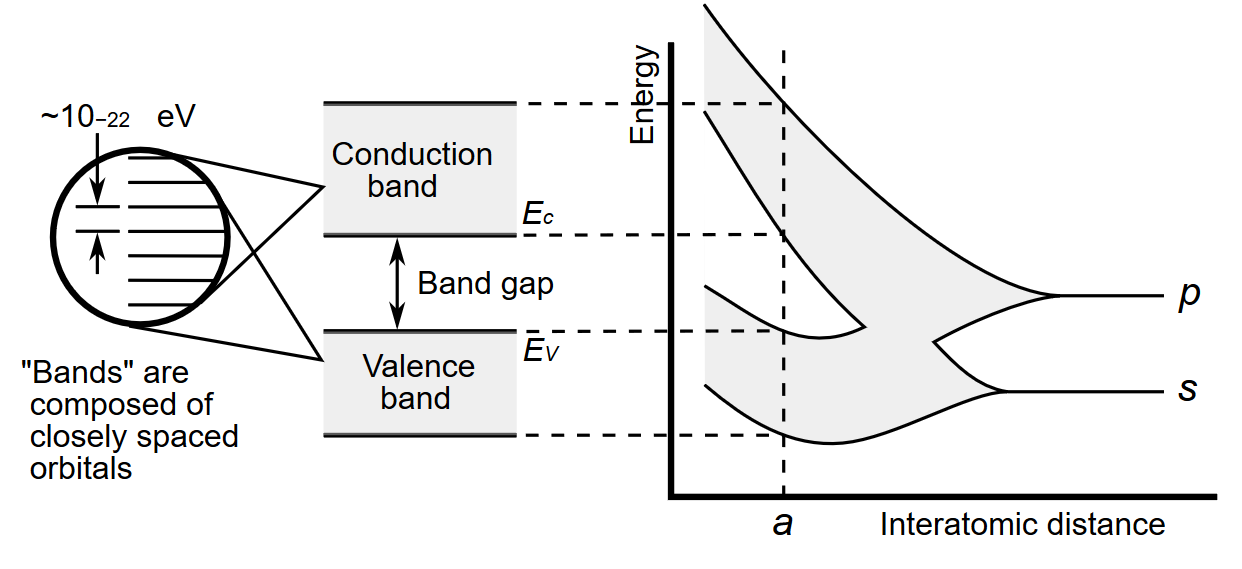
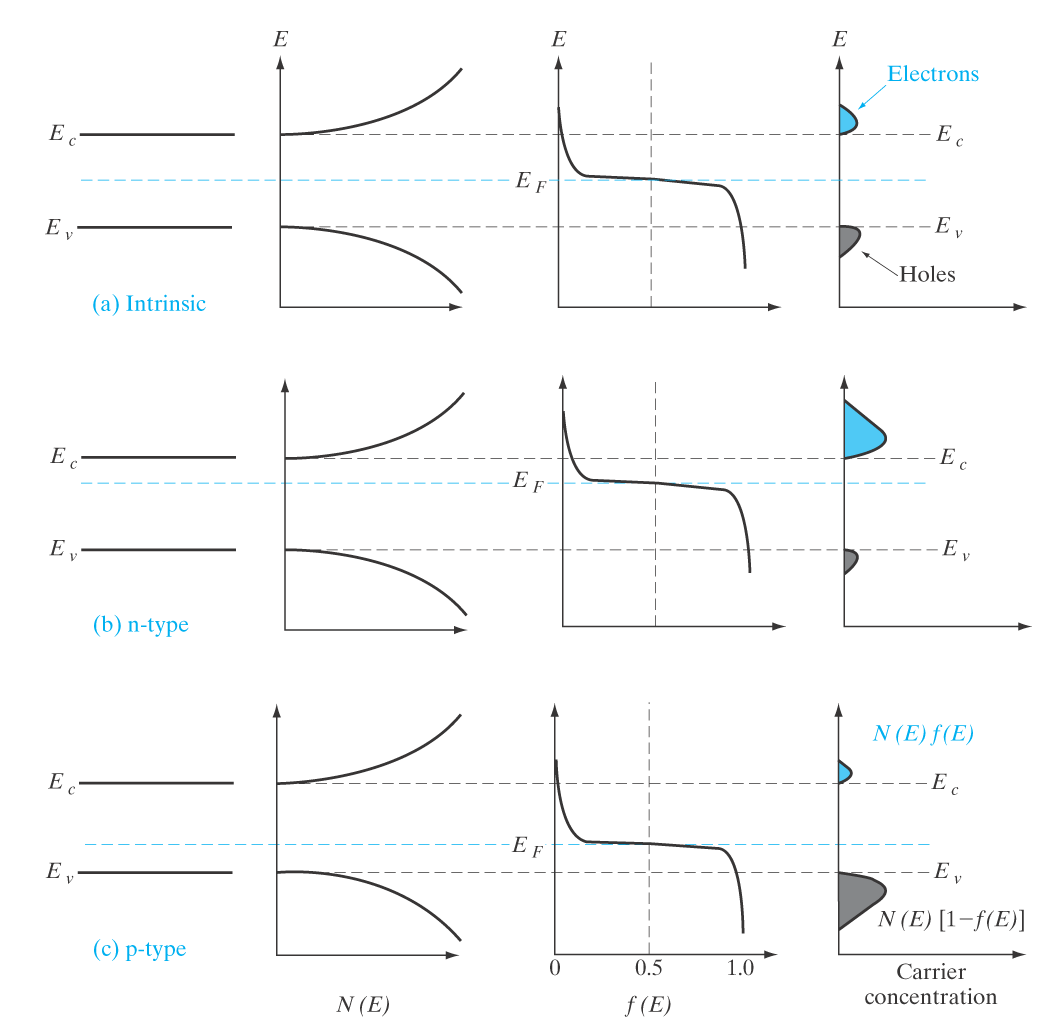
Hvordan beskrive hvordan e^- og h^+ er fordelt i CB og VB.

 \delta n(E) = N(E) \cdot f(E) \cdot \delta E 

Der

• \delta n(E) er tettheten av e^- i CB.
• N(E) er mulige av elektrontilstander
• f(E) er Fermi-Dirac sannsynlighetsfordelingen
• \delta E er energidifferansen vi ser på. I tilfellet over, er det E_g.

Finnes flere typer

• Isotropisk båndstruktur
• Anisotropisk båndstruktur

 N_C(E) = 4\pi \left(\frac{2m^*}{h^2}\right)^{\frac{3}{2}}\cdot E^\frac{1}{2} 

Fermi-Dirac

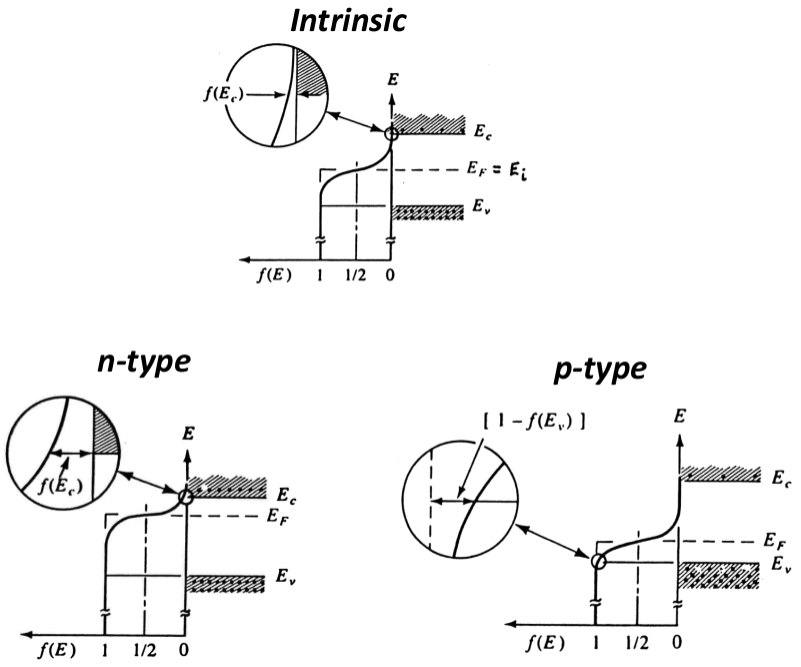
 f(E) = \frac{1}{1 + \exp{\frac{E - E_F}{k_B T}}} 

Fermi-Dirac ved forskjellige dopinger

I et intrinsisk materiale ligger fordelingen midt i båndapet. For en n-type doping vil fordelingen bevege seg mot CB, og i p-type vil den bevege seg mot VB.

Frie elektroner og hull

Ved å se på "summen" av elektrontilstander, N_C og sannsynligheten for å finne dem der.

 \int_{0}^\infty f(E)N_C(E) dE 

Gir oss en likning for frie elektroner i termisk likevet.

 n_0 = \underbrace{2\left(\frac{2\pi m_n^* k_B T}{h^2}\right)^\frac{3}{2}}_{N_c} e^{-\frac{E_C - E_F}{k_B T}} 

Som forkortet, og på samme måte for p_0

 n_0 = N_c e^{-\frac{E_C - E_F}{k_B T}}, \qquad N_c = 2\left(\frac{2\pi m_n^* k_B T}{h^2}\right)^\frac{3}{2} 

 p_0 = N_v e^{-\frac{E_F - E_V}{k_B T}}, \qquad N_v = 2\left(\frac{2\pi m_p^* k_B T}{h^2}\right)^\frac{3}{2} 

Noen resultater

 n_0 p_0 = N_c N_v e^{-\frac{E_g}{k_B T}} 

 n_i p_i = N_c N_v e^{-\frac{E_g}{k_B T}} 

Som sammen med n_i = p_i, gir følgende:

 n_0 p_0 = n_i^2 

Dette gir oss igjen

 n_0 = n_i e^{-\frac{E_F - E_i}{k_B T}} 

 p_0 = n_i e^{-\frac{E_i - E_F}{k_B T}} 

Noen eksempler på bærertetthet

Drift av ladningsbærere

Drifter i alle retninger, ikke noen som er preferert. Litt som en biesverm.

Dersom det påtrykkes et elektrisk felt, vil partiklene fremdeles drifte, men de vi ha en netto bevegelse i en retning. Elektroner vil bevege seg mot feltet, og hull vil bevege seg med.

Strømmen er beskrevet av følgende:

 J_x = q(n\mu_n + p\mu_p)E_x 

Der

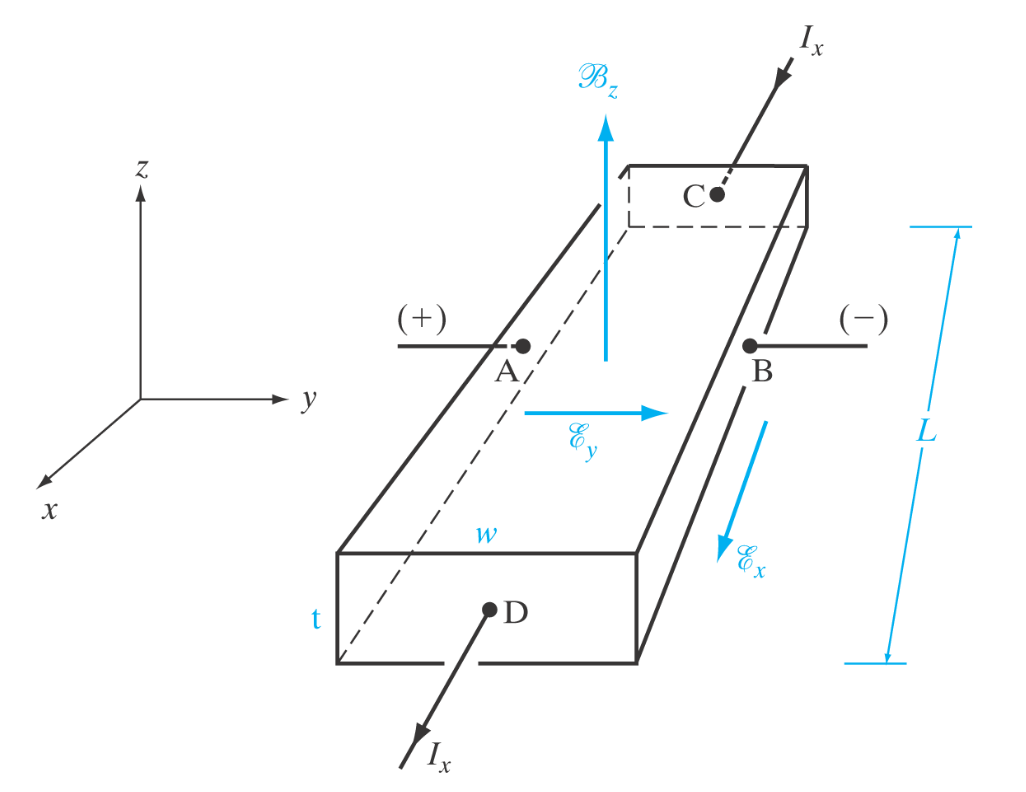
 \mu_n = \frac{q \tau}{m_n^*} \quad \text{og} \quad \mu_p = \frac{q \tau}{m_p^*} 

Hall-effekten

Halleffekten kan brukes til å se på mobiliteten til majoritetsladningsbærerene. F.eks. hull i p-type er majoritetsladningsbærere.

Vi bruker Lortenz kraften, gitt som under:

 \vec{F} = q\left(\vec{E} + \vec{v}\times\vec{B}\right)

Ved påtrykt strømm, J_x og magnetfelt B vil det settes opp et elektrisk felt mellom kontaktene A og B.

La halvlederen være en p-type, da vil, pga. Lorenz-kraften gjøre at hull beveger seg mot kontakten A. Og dermed lage et målbart elektrisk felt fra A til B.

Motsatt felt for n-type med samme strøm og magnetfelt.

Tettheten vil da være gitt som under.

 E_y = \frac{J_x}{qp_0}B_z = R_H J_x B_z 

 R_H \equiv \frac{1}{qp_0} 

Som gir følgende

 p_0 = \frac{I_x B_z}{q t V_{AB}} 

Diffusjon

Natrulig prosess , som å blande melk i kaffe/te eller hvordan oksygen tas opp i kroppen.

Diffusjon er å utligne konsentrasjonsforskjeller over tid, ved bruk av en tilfeldig prosess.

To viktige parameter i diffusjon:

• Spredningstiden \tau, gjennomsnittlig spredningsintervall
• Spredningslengden \bar{l}, gjennomsnittlig lengde mellom spredninger

Elektronfluxen gitt av diffusjon

For elektroner:

 \phi_n(x) = -D_n \frac{dn(x)}{dx}, \quad \text{der } D_n = \frac{\bar{l}^2}{2\tau} 

For hull:

 \phi_p(x) = -D_p \frac{dp(x)}{dx}, \quad \text{der } D_n = \frac{\bar{l}^2}{2\tau} 

D_n og D_p kalles diffusjonskonstantene.

Strømmen gitt av diffusjon

For elektroner:

 J_n^\text{diff} = q D_n \frac{dn(x)}{dx} 

For hull:

 J_p^\text{diff} = -q D_p \frac{dp(x)}{dx} 

Strømmen gitt av diffusjon med påsatt elektrisk felt

For elektroner:

 J_n(x) = q\mu_n n(x) E(x) + q D_n \frac{dn(x)}{dx} 

For hull:

 J_p(x) = q\mu_p p(x) E(x) - q D_p \frac{dp(x)}{dx} 

Der summen av disse gir den totale strømmen:

 J(x) = J_n(x) + J_p(x) 

Einsteinrealasjonen

I termisk likevekt går det ingen netto strøm. Dermed må det settes opp et E-felt for å kompensere driftsstrømmen.

 J_p(x) = q\mu_p p(x) E(x) - q D_p \frac{dp(x)}{dx} = 0 

Som gir:

\begin{align*} E(x) &= \frac{D_p}{\mu_p}\cdot \frac{1}{p_0(x)}\cdot \frac{dp(x)}{dx} \\\ E(x) &= \frac{D_p}{\mu_p}\cdot \frac{1}{k_B T}\left(\frac{dE_i(x)}{dx} - \frac{dE_F(x)}{dx} \right) \end{align*}

Ved termisk likevekt er \frac{dE_F(x)}{dx} = 0 og \frac{dE_i(x)}{dx} = qE(x). Dermed får vi Einsteinrelasjonen:

 \frac{D}{\mu} = \frac{k_B T}{q} 

Kontinuitetslikningen

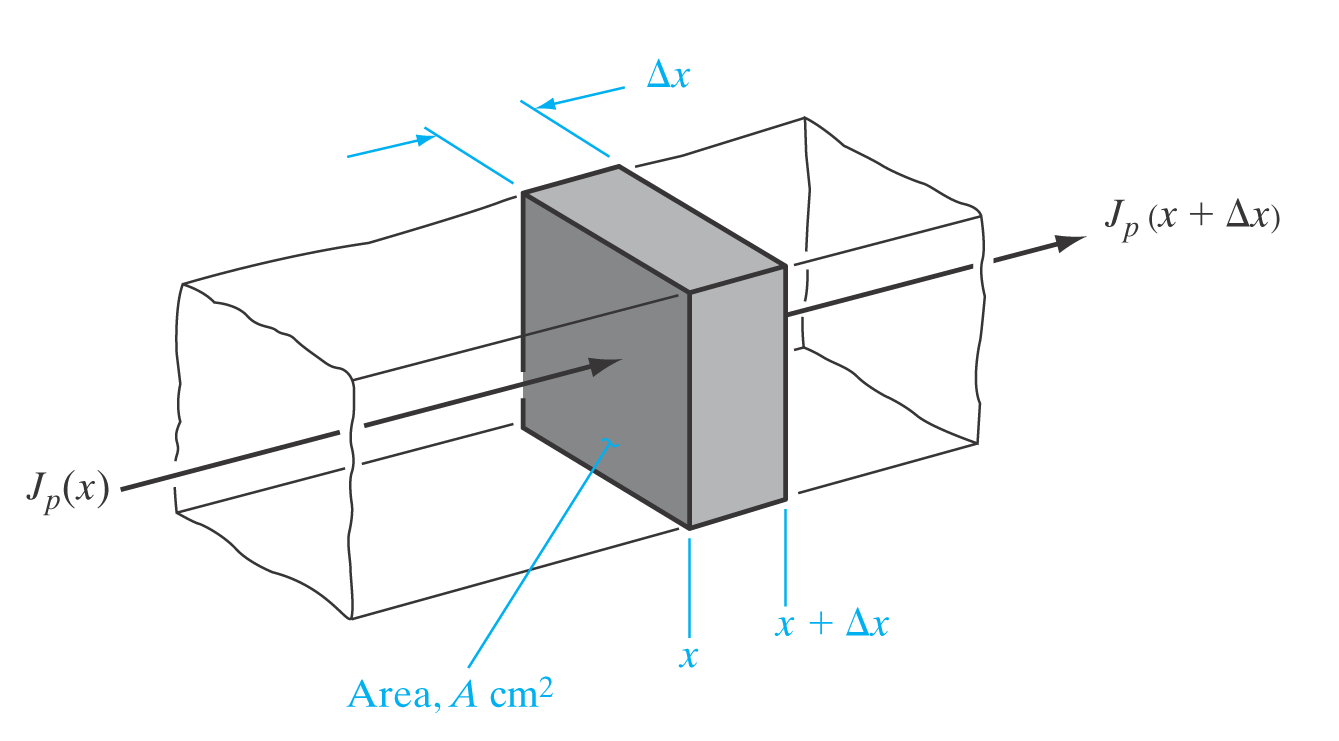
Viser sammenheng mellom endring i hulltetthet og strømmenm gjennom et areale.

 \frac{\partial \delta n(x,t)}{\partial t} = \phantom{-}\frac{1}{q}\frac{\partial J_n(x,t)}{\partial x} - \frac{\delta n}{\tau_n} 

 \frac{\partial \delta p(x,t)}{\partial t} = -\frac{1}{q}\frac{\partial J_p(x,t)}{\partial x} - \frac{\delta p}{\tau_p} 

Steady State

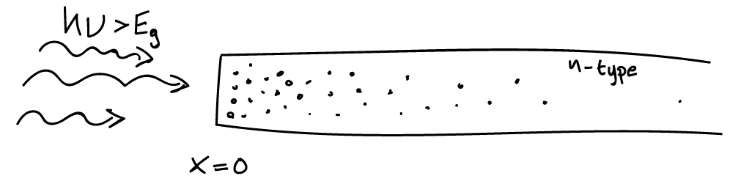
Anta det lyses, med konstant effekt, på ene enden av en bit med n-type halvleder.

Man kan videre anta at det er en konstant hulltetthet på enden med lyset.

 \delta p(x=0) = \Delta p 

Fra diffusjon kan man anta at hullene diffunderer ut over i biten. Siden det ikke er noen tidsavhengighet i hullkonsentrajsonen vil diffusjonsliknignen bli:

 \frac{d^\delta p}{dx^2} = \frac{\delta p}{D_p \tau_p} \equiv \frac{\delta p}{L_p^2} 

Der L_p \equiv \sqrt{D_p \tau_p} .

Denne har en generell løsning:

 \delta p = C_1 \exp{\frac{x}{L_p}} + C_2 \exp{\frac{-x}{L_p}} 

Og med grensebetingelser, \delta p(x=0) = \Delta p og \delta p(x \rightarrow \infty) = 0, gir det oss:

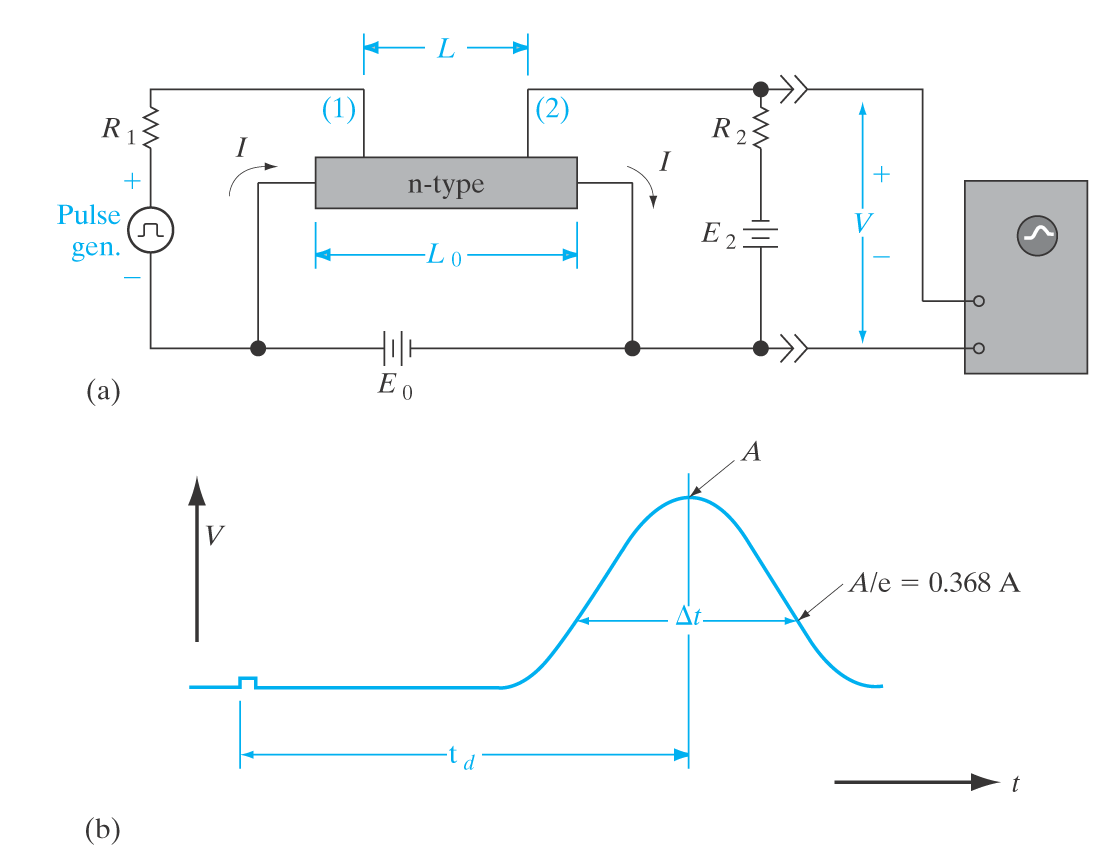
 \delta p(x) = \Delta p \exp{\frac{-x}{L_p}} 

Haynes-Shockley eksperimentet

Eksperiment som gir informasjon om minoritetsladningsbærere.

Vi bruker prinsippet om steady state for å finne mobiliteten til minoritetsladningsbærere og diffusjonskonstanten.

Ved å trykke på en strøm på ene siden, vil vi få et E-felt over halvlederen. Ved å deretter sende inn en lyspuls på ene enden, vil det kunne detekteres en utsmørt versjon av pulsen etter en tid t_d.

PN-overganger