glados.no/ntnu/tfe4146/summary/summary.md

title	description	math	date	toc
Oppsumering av TFE4146	Oppsummering av faget TFE4146 høsten 2020.	true	2020-11-20	true

{% include utilities/toc.html %}

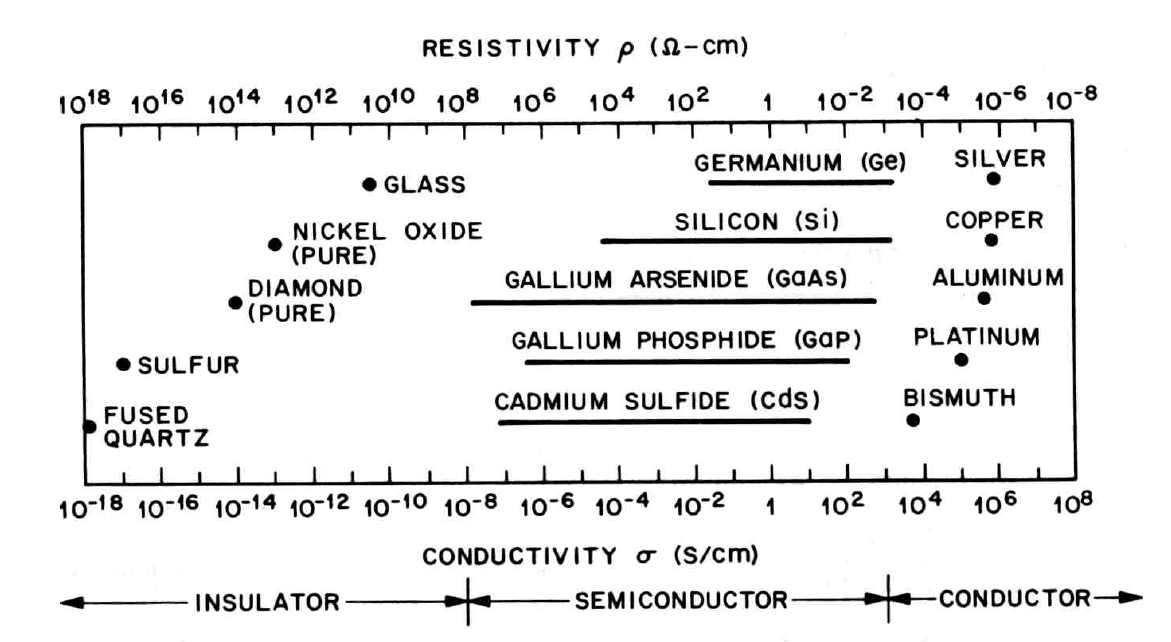
Grunnleggende om halvledere

Historie

• 1830 - Mekanisk
• 1944 - Elektromekanisk
• 1946 - Releer og radiorør
• 1948 - Transistor
• 1958 - Første IC
• 1971 - Første mikroprosessor
• 2020 - Der i er i dag med nanoelektronikk

Moores lov forutser hvor mange transistorer det er plass til per areal. Skal dobles hver 18-24 måneder.

Halvledere

Atomer og elektroner

Uskarphetsrelasjonen

 \Delta x \cdot \delta p_x \geq \frac{\hbar}{2} 

Paulti prinsippet

To like fermioner kan ikke ha den samme kvantetilstanden.

Schrödingers likning

 
\begin{align*}
    - \frac{\hbar ^2}{2m}\frac{\partial^2 \Psi(x,t)}{\partial x^2} &+ V(x)\Psi(x,t) \\
    & = -\frac{\hbar}{j}\frac{\hbar ^2}{2m}\frac{\partial \Psi(x,t)}{\partial t}
\end{align*}

Løsninger

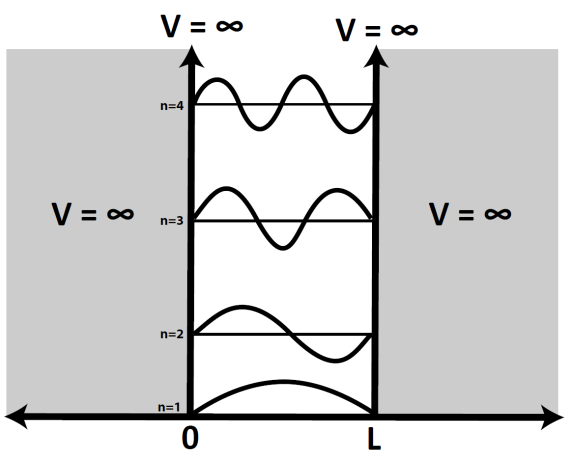
 \psi(x) = Ae^{\pm ikx} \quad E= \frac{\hbar^2 k^2}{2m}

Partikkel i en "boks".

Effektiv masse

 m^* = \frac{\hbar ^2}{\frac{d^2 E}{d k^2}} 

Ser på krumningen til energien i k-rommet. Høy kromming er liten effektiv masse, og vica versa.

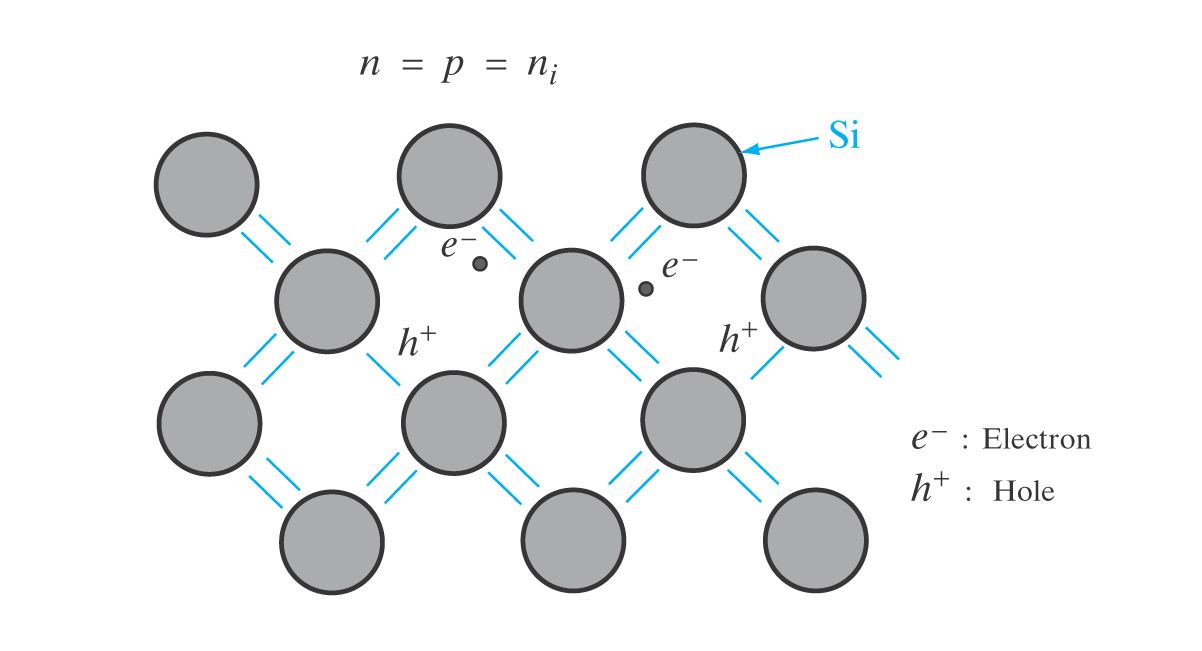
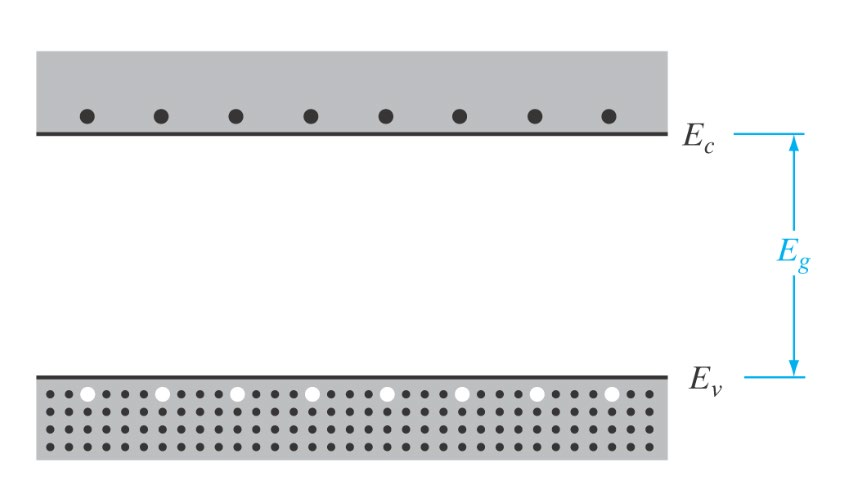
Intrisisk materiale

Inneholder bare en type materiale.

 n = p = n_i 

Der n er tettheten av frie elektroner i lednignsbånd (CB), målt i \text{cm}^{-3}. p er tettheten av hull i valensbåndet (VB), målt i \text{cm}^{-3}. Og n_i er den intrisiske elektrontettheten, målt i \text{cm}^{-3}.

Ekstrinsiske materialer

Disse er intrinsiske materialer som er dopet med et donor eller akseptor materiale.

I Si er det typisk As (Arsenik, donor), eller B (Bor, akseptor).

n-type

 n_0 \gg p_0,n_i 

Der n_0 er elektrontettheten i termisk likevekt.

p-type

 p_0 \gg n_0,n_i 

Der n_0 er elektrontettheten i termisk likevekt.

Elektron-Hull-par i intrinsiske materialer

Elektroner og hull genereres og rekominerer kontinuerlig.

 r_i = g_i 

 r_i = \alpha n_0 p_0 = \alpha n_i^2 = g_i 

Bærertetthet

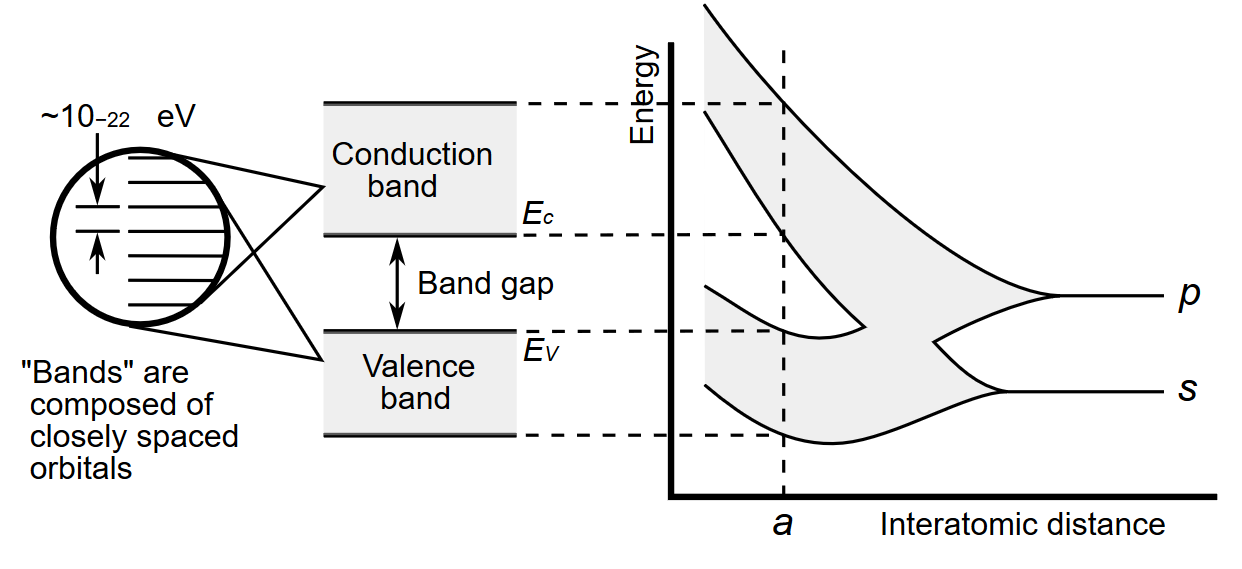
Hvordan beskrive hvordan e^- og h^+ er fordelt i CB og VB.

 \delta n(E) = N(E) \cdot f(E) \cdot \delta E 

Der

• \delta n(E) er tettheten av e^- i CB.
• N(E) er mulige av elektrontilstander
• f(E) er Fermi-Dirac sannsynlighetsfordelingen
• \delta E er energidifferansen vi ser på. I tilfellet over, er det E_g.

Finnes flere typer

• Isotropisk båndstruktur
• Anisotropisk båndstruktur

 N_C(E) = 4\pi \left(\frac{2m^*}{h^2}\right)^{\frac{3}{2}}\cdot E^\frac{1}{2} 

Fermi-Dirac

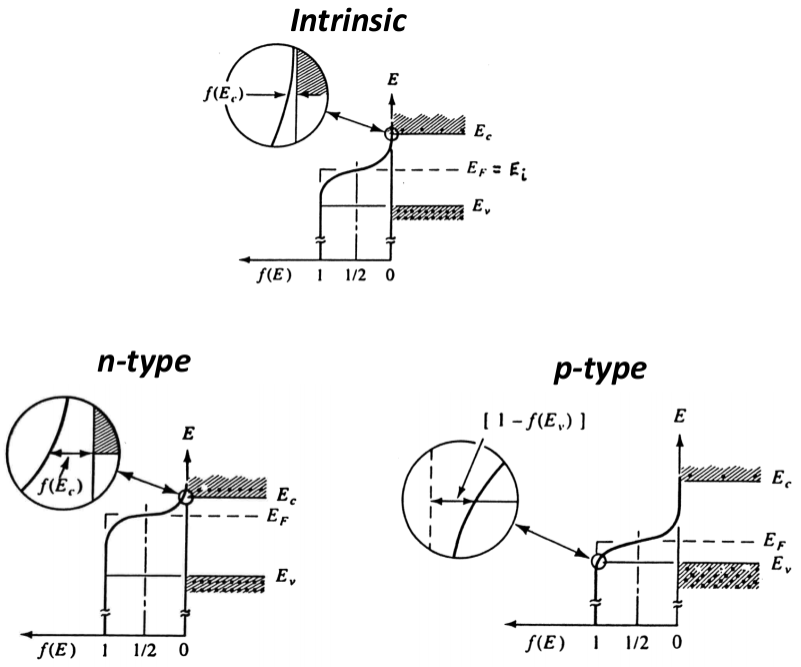
 f(E) = \frac{1}{1 + \exp{\frac{E - E_F}{k_B T}}} 

Fermi-Dirac ved forskjellige dopinger

I et intrinsisk materiale ligger fordelingen midt i båndapet. For en n-type doping vil fordelingen bevege seg mot CB, og i p-type vil den bevege seg mot VB.

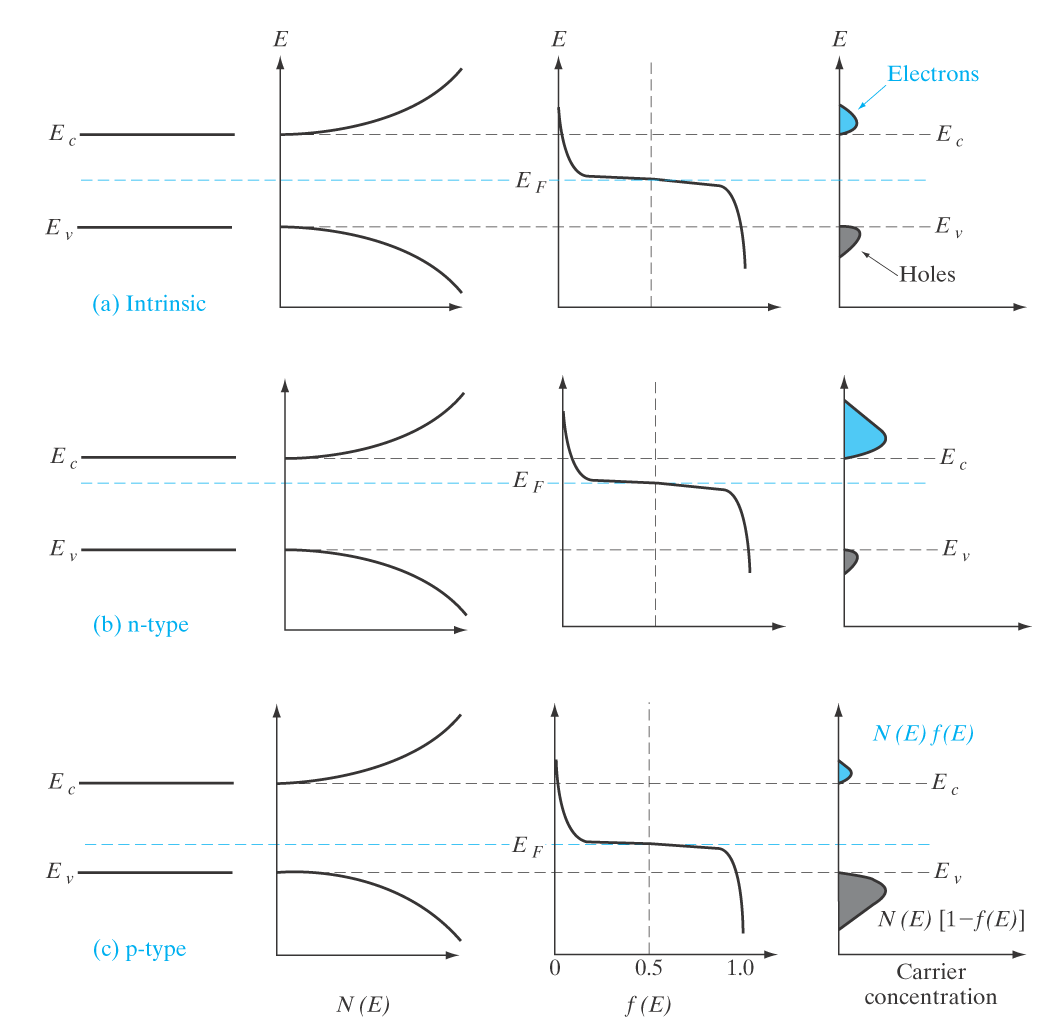
Frie elektroner og hull

Ved å se på "summen" av elektrontilstander, N_C og sannsynligheten for å finne dem der.

 \int_{0}^\infty f(E)N_C(E) dE 

Gir oss en likning for frie elektroner i termisk likevet.

 n_0 = \underbrace{2\left(\frac{2\pi m_n^* k_B T}{h^2}\right)^\frac{3}{2}}_{N_c} e^{-\frac{E_C - E_F}{k_B T}} 

Som forkortet, og på samme måte for p_0

 n_0 = N_c e^{-\frac{E_C - E_F}{k_B T}}, \quad N_c = 2\left(\frac{2\pi m_n^* k_B T}{h^2}\right)^\frac{3}{2} 

 p_0 = N_v e^{-\frac{E_F - E_V}{k_B T}}, \quad N_v = 2\left(\frac{2\pi m_p^* k_B T}{h^2}\right)^\frac{3}{2} 

Noen resultater

 n_0 p_0 = N_c N_v e^{-\frac{E_g}{k_B T}} 

 n_i p_i = N_c N_v e^{-\frac{E_g}{k_B T}} 

Som sammen med n_i = p_i, gir følgende:

 n_0 p_0 = n_i^2 

Dette gir oss igjen

 n_0 = n_i e^{-\frac{E_F - E_i}{k_B T}} 

 p_0 = n_i e^{-\frac{E_i - E_F}{k_B T}} 

Noen eksempler på bærertetthet

Drift av ladningsbærere

Drifter i alle retninger, ikke noen som er preferert. Litt som en biesverm.

Dersom det påtrykkes et elektrisk felt, vil partiklene fremdeles drifte, men de vi ha en netto bevegelse i en retning. Elektroner vil bevege seg mot feltet, og hull vil bevege seg med.

Strømmen er beskrevet av følgende:

 J_x = q(n\mu_n + p\mu_p)E_x 

Der

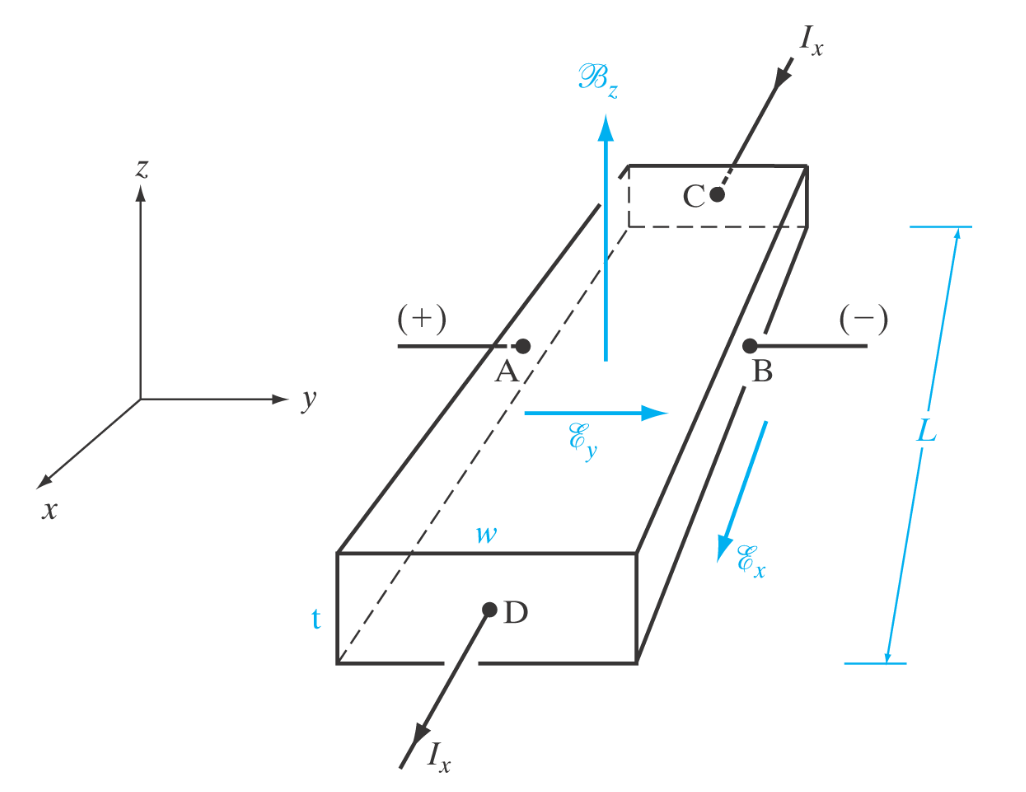
 \mu_n = \frac{q \tau}{m_n^*} \quad \text{og} \quad \mu_p = \frac{q \tau}{m_p^*} 

Hall-effekten

Halleffekten kan brukes til å se på mobiliteten til majoritetsladningsbærerene. F.eks. hull i p-type er majoritetsladningsbærere.

Vi bruker Lortenz kraften, gitt som under:

 \vec{F} = q\left(\vec{E} + \vec{v}\times\vec{B}\right)

Ved påtrykt strømm, J_x og magnetfelt B vil det settes opp et elektrisk felt mellom kontaktene A og B.

La halvlederen være en p-type, da vil, pga. Lorenz-kraften gjøre at hull beveger seg mot kontakten A. Og dermed lage et målbart elektrisk felt fra A til B.

Motsatt felt for n-type med samme strøm og magnetfelt.

Tettheten vil da være gitt som under.

 E_y = \frac{J_x}{qp_0}B_z = R_H J_x B_z 

 R_H \equiv \frac{1}{qp_0} 

Som gir følgende

 p_0 = \frac{I_x B_z}{q t V_{AB}} 

Diffusjon

Natrulig prosess , som å blande melk i kaffe/te eller hvordan oksygen tas opp i kroppen.

Diffusjon er å utligne konsentrasjonsforskjeller over tid, ved bruk av en tilfeldig prosess.

To viktige parameter i diffusjon:

• Spredningstiden \tau, gjennomsnittlig spredningsintervall
• Spredningslengden \bar{l}, gjennomsnittlig lengde mellom spredninger

Elektronfluxen gitt av diffusjon

For elektroner:

 \phi_n(x) = -D_n \frac{dn(x)}{dx}, \quad \text{der } D_n = \frac{\bar{l}^2}{2\tau} 

For hull:

 \phi_p(x) = -D_p \frac{dp(x)}{dx}, \quad \text{der } D_n = \frac{\bar{l}^2}{2\tau} 

D_n og D_p kalles diffusjonskonstantene.

Strømmen gitt av diffusjon

For elektroner:

 J_n^\text{diff} = q D_n \frac{dn(x)}{dx} 

For hull:

 J_p^\text{diff} = -q D_p \frac{dp(x)}{dx} 

Strømmen gitt av diffusjon med påsatt elektrisk felt

For elektroner:

 J_n(x) = q\mu_n n(x) E(x) + q D_n \frac{dn(x)}{dx} 

For hull:

 J_p(x) = q\mu_p p(x) E(x) - q D_p \frac{dp(x)}{dx} 

Der summen av disse gir den totale strømmen:

 J(x) = J_n(x) + J_p(x) 

Einsteinrealasjonen

I termisk likevekt går det ingen netto strøm. Dermed må det settes opp et E-felt for å kompensere driftsstrømmen.

 J_p(x) = q\mu_p p(x) E(x) - q D_p \frac{dp(x)}{dx} = 0 

Som gir:

\begin{align*}
    E(x) &= \frac{D_p}{\mu_p}\cdot \frac{1}{p_0(x)}\cdot \frac{dp(x)}{dx} \\
    E(x) &= \frac{D_p}{\mu_p}\cdot \frac{1}{k_B T}\left(\frac{dE_i(x)}{dx} - \frac{dE_F(x)}{dx} \right)
\end{align*}

Ved termisk likevekt er \frac{dE_F(x)}{dx} = 0 og \frac{dE_i(x)}{dx} = qE(x). Dermed får vi Einsteinrelasjonen:

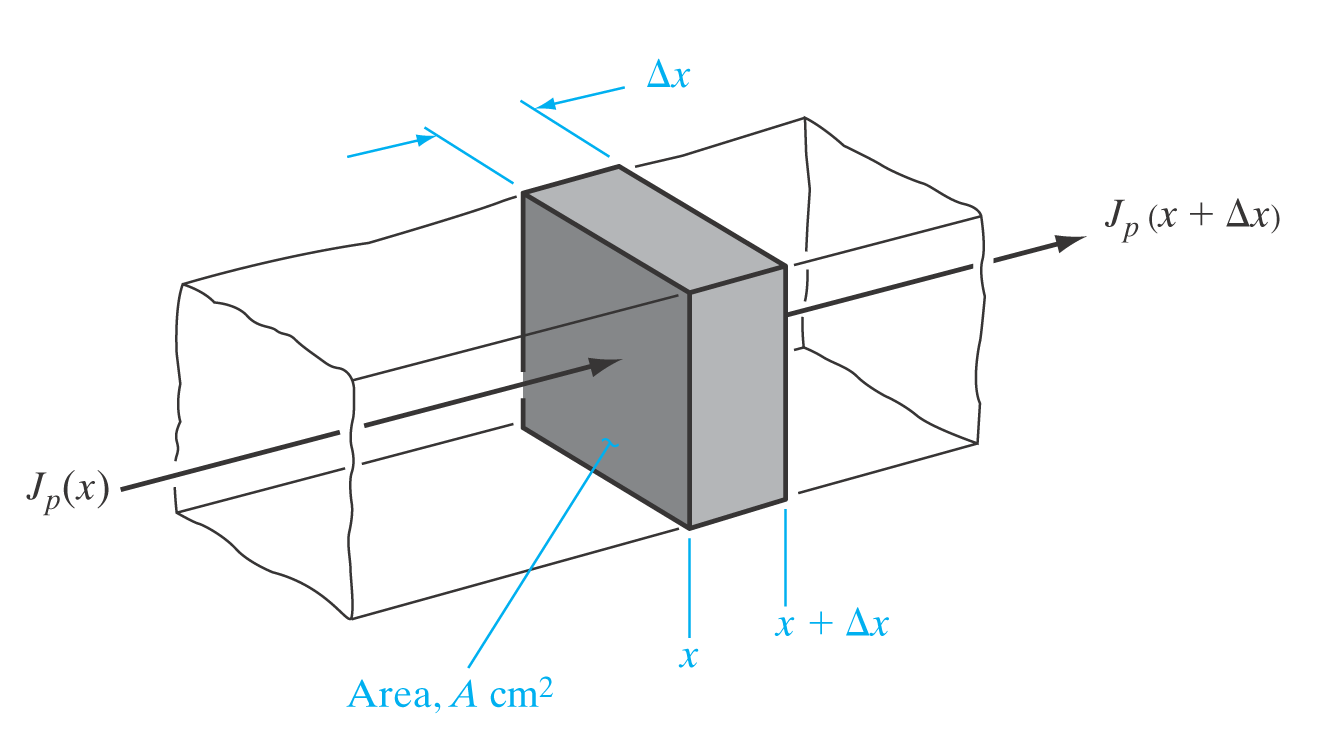
 \frac{D}{\mu} = \frac{k_B T}{q} 

Kontinuitetslikningen

Viser sammenheng mellom endring i hulltetthet og strømmenm gjennom et areale.

 \frac{\partial \delta n(x,t)}{\partial t} = \phantom{-}\frac{1}{q}\frac{\partial J_n(x,t)}{\partial x} - \frac{\delta n}{\tau_n} 

 \frac{\partial \delta p(x,t)}{\partial t} = -\frac{1}{q}\frac{\partial J_p(x,t)}{\partial x} - \frac{\delta p}{\tau_p} 

Steady State

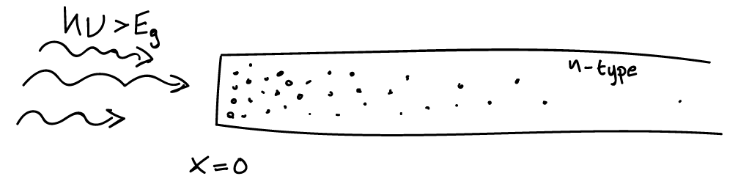
Anta det lyses, med konstant effekt, på ene enden av en bit med n-type halvleder.

Man kan videre anta at det er en konstant hulltetthet på enden med lyset.

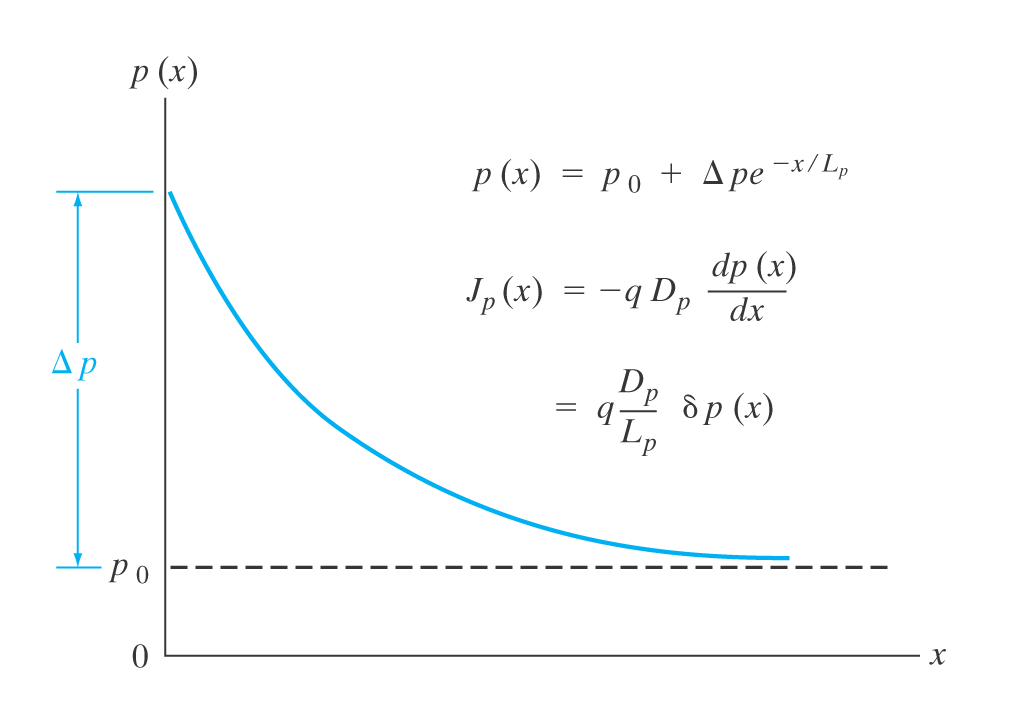
 \delta p(x=0) = \Delta p 

Fra diffusjon kan man anta at hullene diffunderer ut over i biten. Siden det ikke er noen tidsavhengighet i hullkonsentrajsonen vil diffusjonsliknignen bli:

 \frac{d^\delta p}{dx^2} = \frac{\delta p}{D_p \tau_p} \equiv \frac{\delta p}{L_p^2} 

Der L_p \equiv \sqrt{D_p \tau_p} .

Denne har en generell løsning:

 \delta p = C_1 \exp{\frac{x}{L_p}} + C_2 \exp{\frac{-x}{L_p}} 

Og med grensebetingelser, \delta p(x=0) = \Delta p og \delta p(x \rightarrow \infty) = 0, gir det oss:

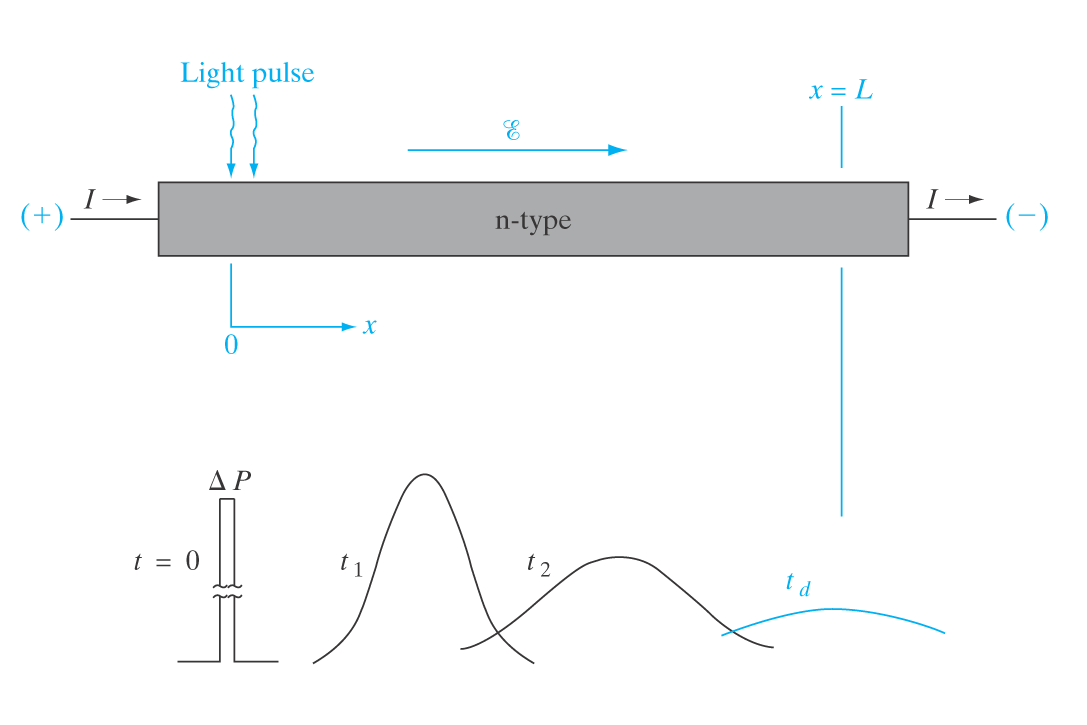
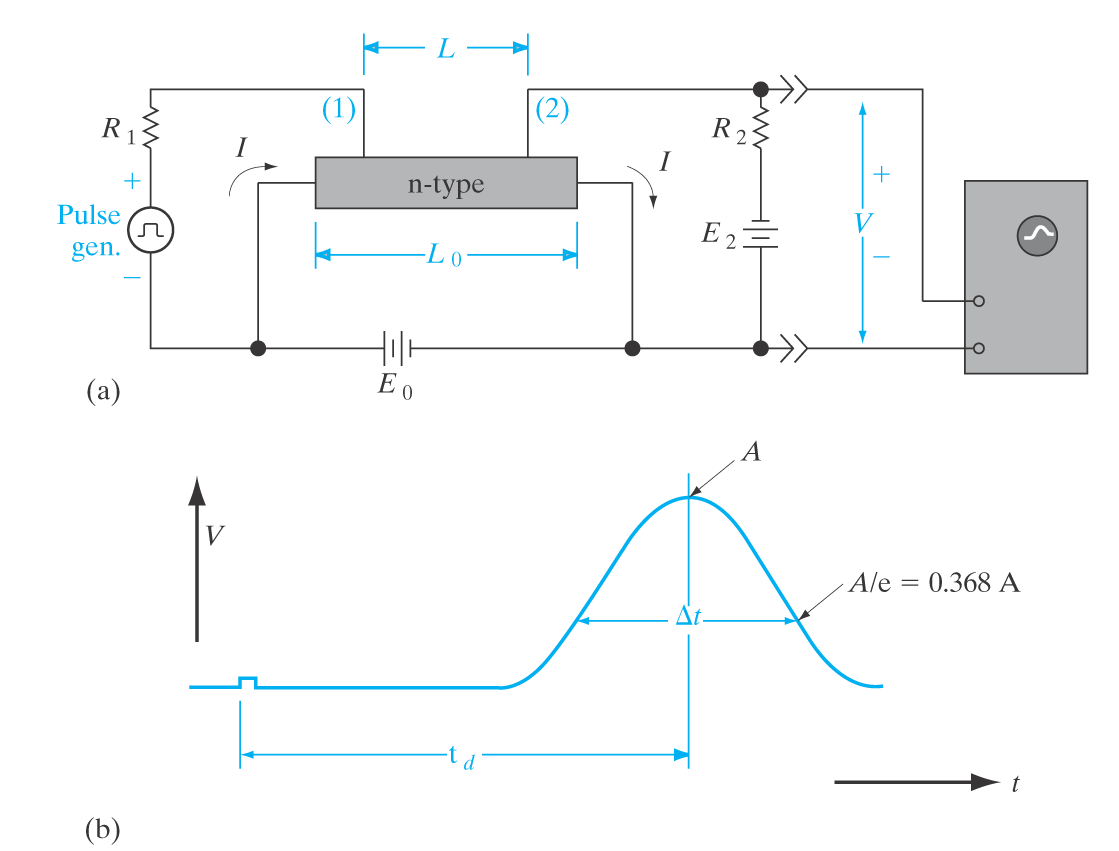
 \delta p(x) = \Delta p \exp{\frac{-x}{L_p}} 

Haynes-Shockley eksperimentet

Eksperiment som gir informasjon om minoritetsladningsbærere.

Vi bruker prinsippet om steady state for å finne mobiliteten til minoritetsladningsbærere og diffusjonskonstanten.

Ved å trykke på en strøm på ene siden, vil vi få et E-felt over halvlederen. Ved å deretter sende inn en lyspuls på ene enden, vil det kunne detekteres en utsmørt versjon av pulsen etter en tid t_d.

P-N-overganger

Bakgrunn

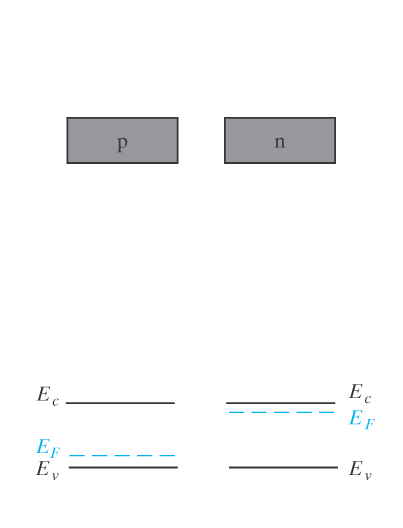
Vi vet at bitene i ugangspunlket er nøytrale. Dermed ved termisk likevekt er følgende sant.

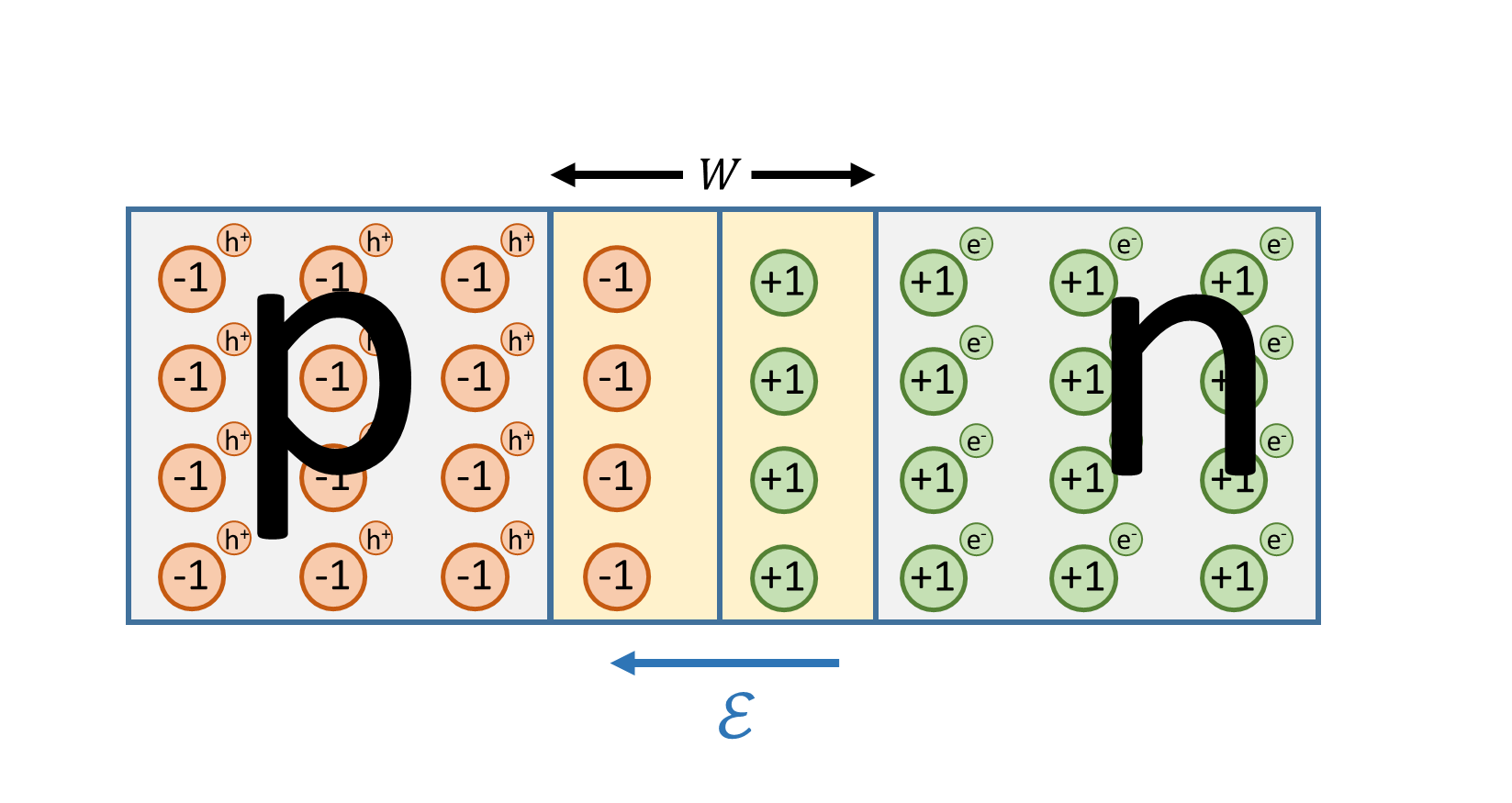
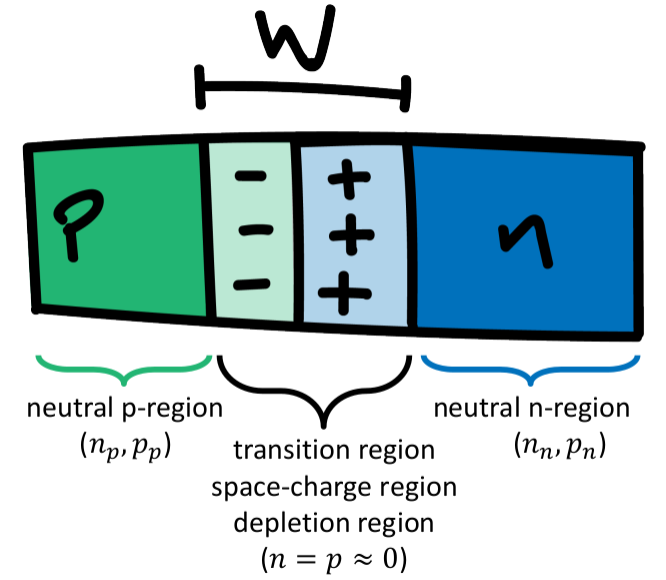
 \frac{d E_F}{ d x} = 0 

 n_n \gg n_p 

 p_p \gg p_n 

Når bitene med dopet silisium blir satt sammen, vil det settes opp et overgangsområde.

For å analysere dette, gjøres det noen forenklinger

1. Stegovergang, skarp p-n-overgang
2. 1D analyse av ladningstransport
3. E-feltet er satt til 0 utenfor overgangsområdet
4. Deplesjonstilnærming

Noen viktige prinsipper

Gauss' lov

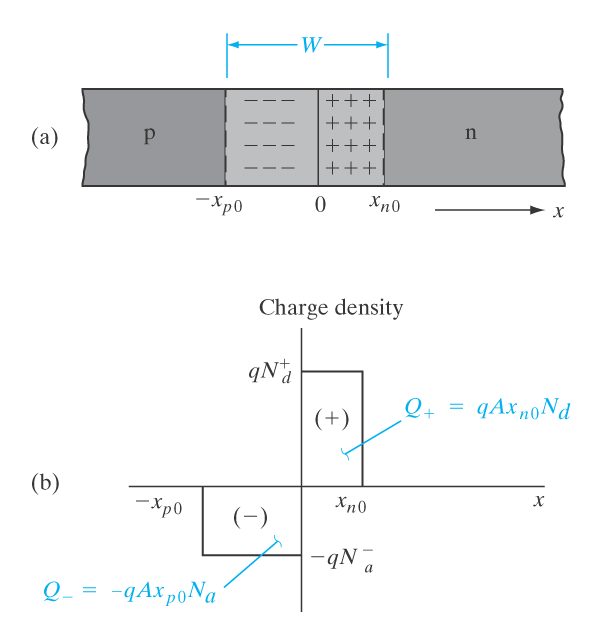
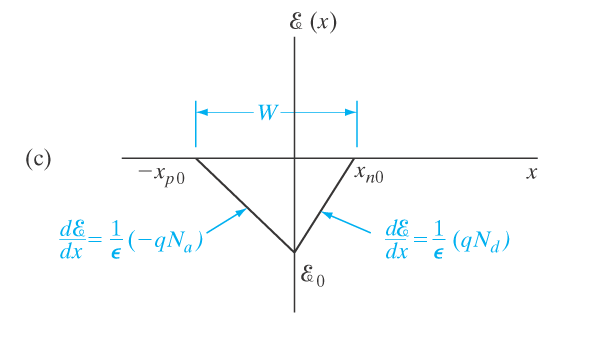
 \frac{d E(x)}{dx} = \frac{q}{\epsilon}\cdot [p(x) - n(x) + N_d^+ - N_a^-] 

Deplesjonstilnærming

\begin{align*}
    p(x) = n(x) &= 0 \quad \text{innenfor }W \\
    \rho(x)     &= 0 \quad \text{utnfor }W  
\end{align*}

\begin{align*} 
    \frac{d E(x)}{dx} &=  \phantom{-}\frac{q}{\epsilon}N_d^+ \quad \text{for } 0 < x < x_{n0} \\
    \frac{d E(x)}{dx} &=  -\frac{q}{\epsilon}N_a^- \quad \text{for } -x_{p0} < x < 0
\end{align*} 

Bredden av deplesjonsområdet

Ved å sette sammen deplesjnstilnærmingen og Guass' sammen får vi et uttrykk for spenningen og bredden på deplesjonsområdet.

 V_0 = \frac{1}{2}E_0 W 

Der E_0 = N_d x_{n0} = N_a x_{p0}.

Som igjen gir

 V_0 = \frac{1}{2}\frac{q}{\epsilon}\frac{N_a N_d}{N_a + N_d} W^2 

Som vi løser for W og får,

 W = \sqrt{\frac{2\epsilon V_0}{q} \cdot \left(\frac{1}{N_a}+ \frac{1}{N_d}\right)} 

Forspent overgang

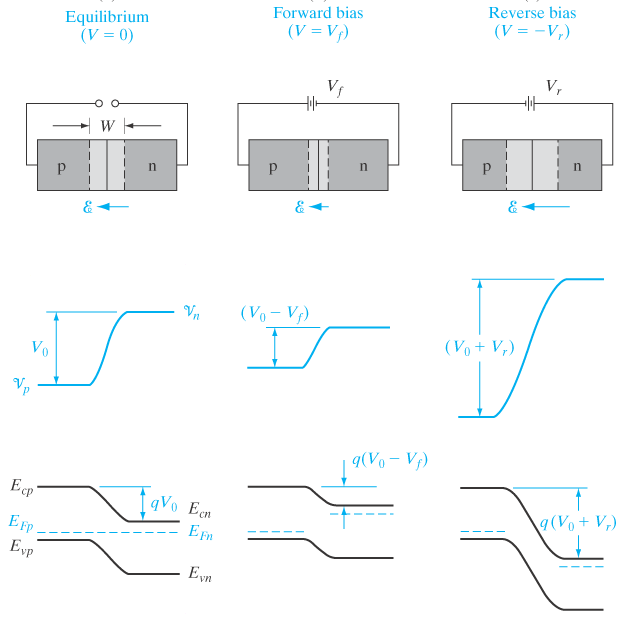
Positiv forspenning er definert som å koble positiv terminal til p-siden og - til n-siden. Negativ forspenning er det motsatte.

Forspenningen vil ha alt spenningsfallet over deplesjonsområdet W. Med andre ord vil E-feltet endre størrelse med forspenningen. Desto større negativ forspenning, desto større E-felt (opp til et visst punkt). For positive forspenninger vil vi minke E-feltet med økt positiv forspenning.

Kvalitativ analyse

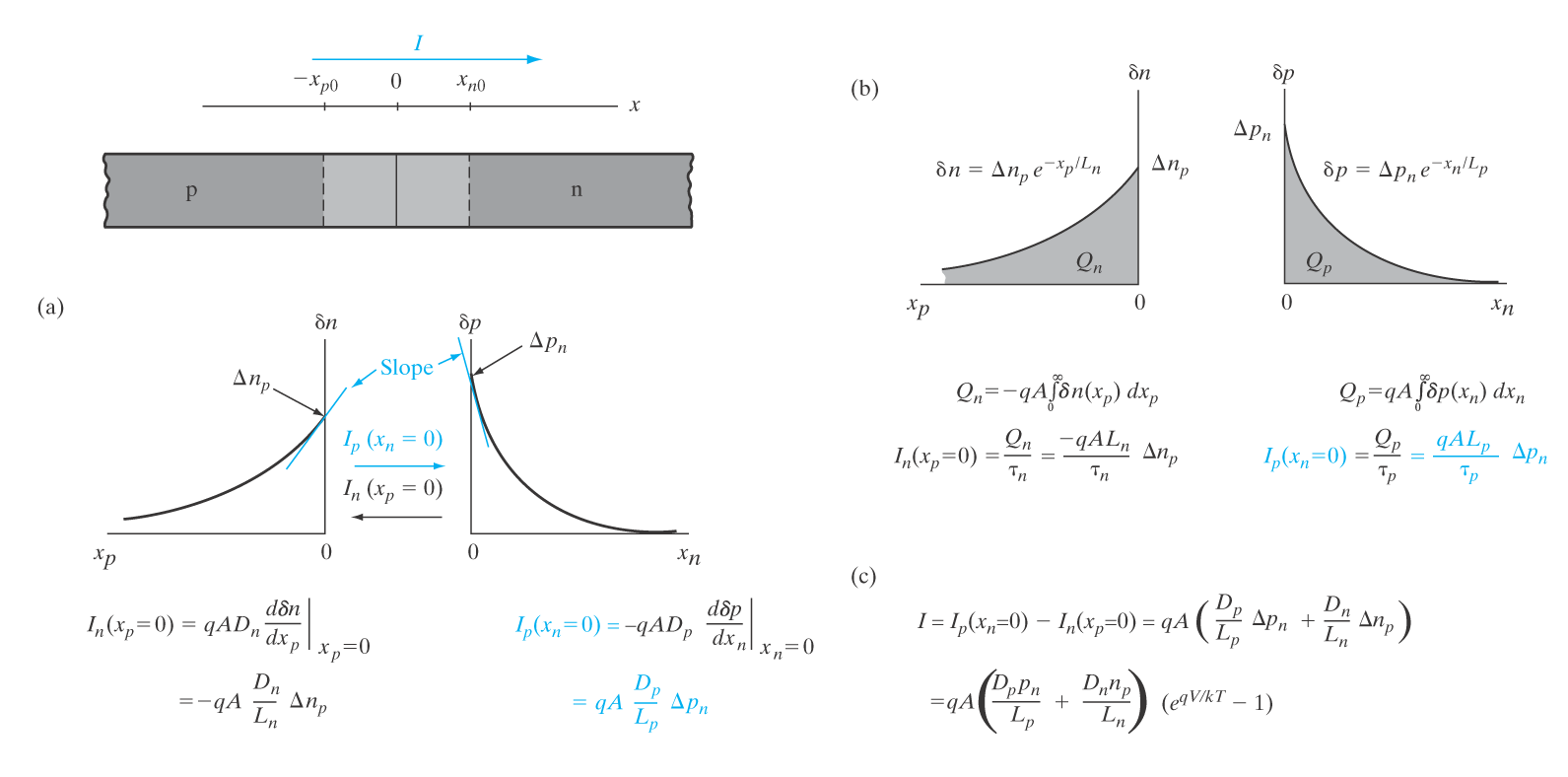
Vi kan nå evaluere hullstrømmen.

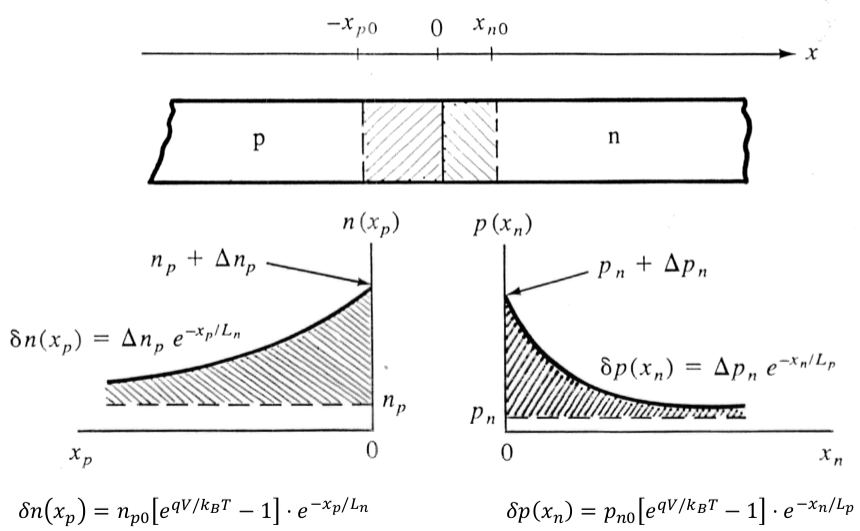
 I_p(x_n) = -qAD_p \frac{d \delta p(x_n)}{d x_n} = qA\frac{D_p}{L_p} \delta p(x_n) 

Der strømmen inn i deplesjonsområdet er gitt ved

 
\begin{align*}
    I_p(x_n = 0)    &= qA\frac{D_p}{L_p}\Delta p_n \\
                    &= qA\frac{D_p}{L_p} p_n \left[\exp{\frac{qV}{k_B T}} - 1\right] 
\end{align*}

For elektroner, er det et minustegn foran, som skifter retningen, men ellers helt lik.

 
\begin{align*}
    I_n(x_p = 0)    &= -qA\frac{D_n}{L_n}\Delta n_p \\
                    &= -qA\frac{D_n}{L_n} n_p \left[\exp{\frac{qV}{k_B T}} - 1\right] 
\end{align*}

Videre bruker vi enda en forenkling:

S6 All strømmen som sendes inn i deplesjonsområdet vil ende opp på andre siden.

\begin{align*}
    I_p(x_p = 0)&= I_p(x_n = 0) \\ 
    I_n(x_p = 0)&= I_n(x_n = 0)
\end{align*}

Dette gir oss en total strøm:

 I = I_p (x_n = 0) + \left(-I_n(x_p = 0)\right) 

Setter alt sammen og får "diodelikningen":

 I = qA\left[ \frac{D_p}{L_p}p_{n0} + \frac{D_n}{L_n}n_{p0} \right] \cdot \left[\exp{\frac{qV}{k_B T}} - 1\right] 

Dersom vi setter I_0\equiv\left[ \frac{D_p}{L_p}p_{n0} + \frac{D_n}{L_n}n_{p0} \right], kan vi skrive:

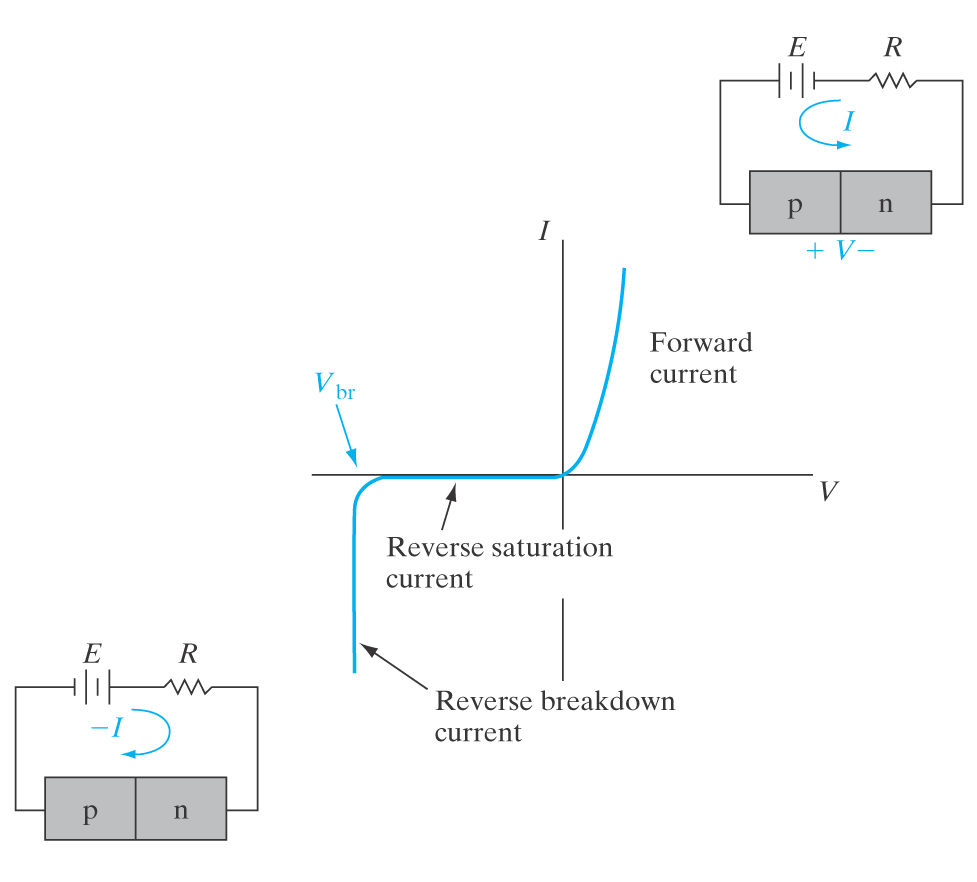
 I = I_0 \left[\exp{\frac{qV}{k_B T}} - 1\right]  

Alternativ måte å løse denne på

Den baserer seg på at det finnes ladninger på hver side av deplesjonsområdet. Det er da mulig å integrere over ladningene og se på gradienten ved x_p = x_n = 0.

Sammenbruddsdioder

Dersom man reversforspenner (negativ forspenning) så vil situasjonen der dioden får et sammenbrudd skje. Sammenbruddet er kun elektronisk og ikke skadelig for dioden, med mindre man setter på veldig mye negativ forspenning.

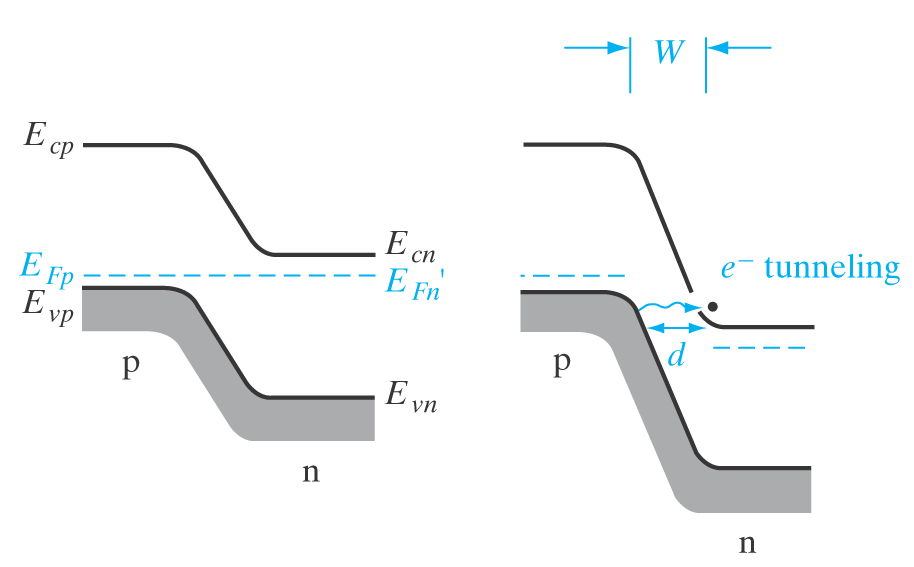
Zenersammenbrudd

Et Zenersammenbrudd baserer seg på kvantetunnelering mellom energibåndene i dioden. Elektronene kan da "hoppe" fra valensbåndet til ledningsbåndet.

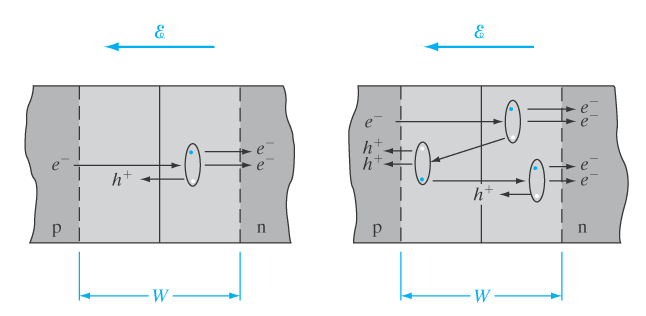
Avalanche Breakdown (Skredsammenbrudd?)

Baserer seg på at ved et stort E-felt i sperreretning vil elektroner få stor hastighet. Når elektronene treffer et atom el. vil den kunne "sparke løs" et annet elektron-hull-par. Dette medfører at det nå er to elektroner i ene retningen og to hull i andre retningen.

Transienter i en p-n-overgang

Stegtransient

Vi vil se på tilfellet der vi skrur av strømmen abrupt ved t=0.

Kommer tilbake til dette...

Forskjellige typer p-n-overganger

Også sees på senere

Felt Effekt Transistorer (FET)

Historie

• 1915 - Første radiorør
• 1926 - Patent på en CuS FET
• 1934 - Design av en FET
• 1947 - Den første transistoren ble laget
• 1954 - Første transistor i Si
• 1959 - Første IC
• 1960 - Første MOSFET
• 1971 - Intel kom med første komersielle mikroprosessor, Intel 4004

Forskjellige typer FET

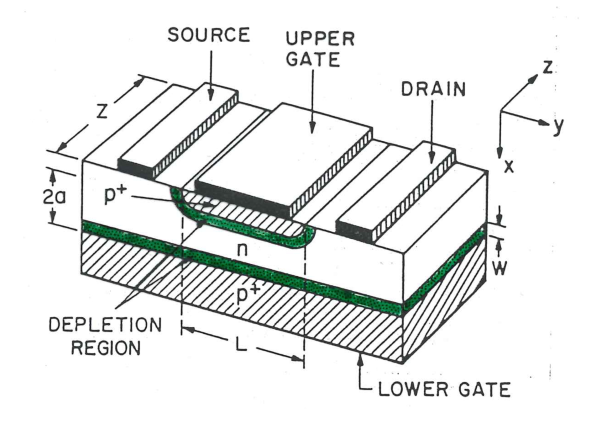
JFET

JFET (Junction Field Effect Transistor), fungerer ved å styre/modulere bredden på deplesjonsområdet på en revers forspent p-n-overgang, ved hjelp av en påsatt spenning V_G. Dette medfører at vi kan kontrollere strømmen mellom kilde (source) og brønn (drain) kontaktene.

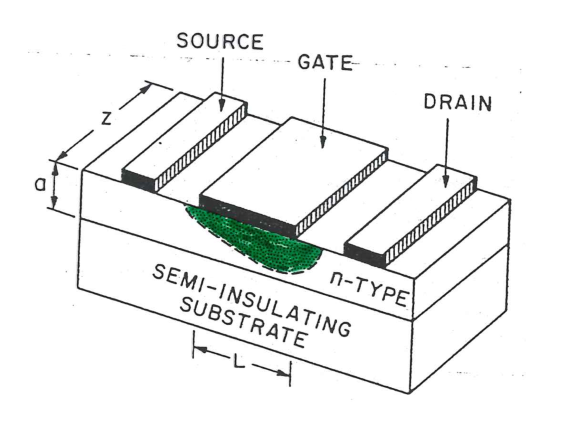
MESFET

Fungerer på samme måte som en JFET, men styrer bredden på deplesjonsområdet i en Schottky diode. Dette er derfor en Metall-Silisium overgang (M-S overgang).

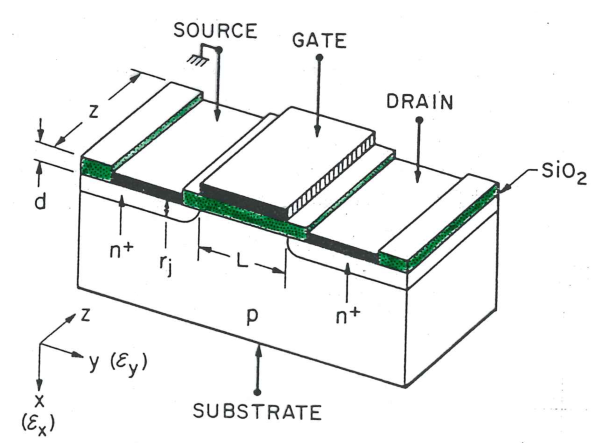
MOSFET

Dette er den mest brukte transistoren i dag. Her er gate-kontakten elektrisk separert fra resten av transistoren med et isolerende lag. Transistoren fungerer da ved å sette opp mellom gate og substratet i transistoren for å lage en elektrisk ledene kanal mellom kilde og brønnkontaktene. Det er derfor den har navnet MOSFET, Metal-Oksid-Silikon Felt Effekt Transistor (Metal-Oxide-Silicon Field Effect Transistor).

Fordeler med FET over BJT

• Høy inngangsimpedanse.
  • I JFET er det pga. en revers forspend p-n-overgang.
  • I MESFET er det pga. en revers forspent m-s-overgang.
  • I MOSFET er det pga. en isolator mellom gate og resten av transistoren.
• Veldig god som en bryter for å styre mellom en ledende tilstand og en ikke ledende tilstand.
• Negativ temperaturkoeffisient ved store strømmer, som gjør den veldig stabil.
• Har ingen lagring av minoritetsladningsbærere, som fører til ingen uønsket kapasitanse.
• Har høyere endringshastighet (switching speed) enn en vanlig BJT.

Virkemåte til en transistor

En transistor har i prinsippet to funksjoner:

1. Forsterkning av små AC-signaler.
2. Som en bryter, for å styre en strøm.

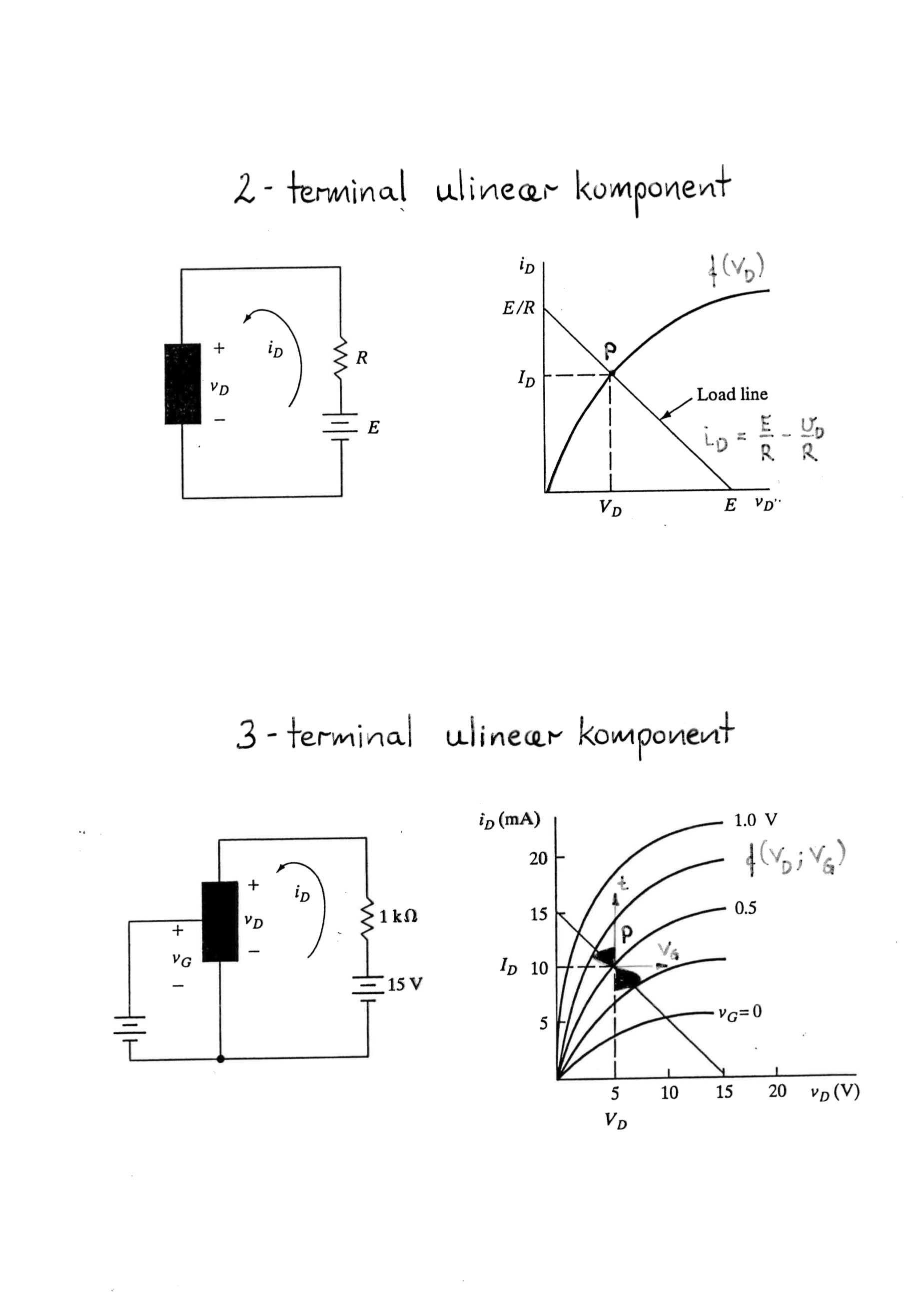
I-V-kurve

Strømmen til en transistor kan beskrives med spenningen over transistoren.

 i_D = f(v_D)

Der lastlinjen er definert som

 i_D = \frac{E}{R} - \frac{v_D}{R} 

For en komponent med to terminaler vil vi kun ha disse likningene, men for en komponent med tre poler kan vi også styre hvordan f(v_D) fungerer ved hjelp av v_G.

JFET