glados.no/ntnu/ttt4120/summary/summary.md

title	description	date	math
Oppsumering av TTT4120	En liten oppsummering og formler i TTT4120, høsten 2020.	2020-12-06	true

Diskret tid

Denne typen signaler baserer seg på at de kan representeres av en sekvens med tall. Sekvensen kan representere amplituden til et signal, ved tidspunkt n.

 x[n] = \{\ldots, x[-1], \underline{x[0]}, x[1], \ldots\} 

Der verdien med strek under er målingen ved n=0.

Sampling

Signalene kan lages ved å sample et analogt signal.

 x[n] \stackrel{_\Delta}{=} x_a(nT)

Der tiden mellom samples er gitt ved T = \frac{1}{F_S}, der samplings-frekvensen (samples per sekund) er F_S.

T trenger ikke å være tid, men f.eks. posisjonen på en stang.

Diskret-tid operasjoner

Skalering, addering, og multiplikasjon:

 
\begin{gather*}
	y[n] = ax[n] \\
	y[n] = x_1[n] + x_2[n] \\
	y[n] = x_1[n]x_2[n]
\end{gather*} 

Tidsforskyvninger og folding

 
\begin{gather*}
	y[n] = x[n-k] \\
	y[n] = -x[n] 
\end{gather*} 

Tidsforskyvninger sammen med folding

 y[n] = x[-n+k] 

Egenskaper til Diskret tid

En sekvens x[n] er kausal dersom:

 x[n] = 0, n<0 

En sekvens x[n] er periodisk med en periode N dersom:

 x[n+N] = x[n], \forall n 

Klassifikasjoner til Diskret tid

En sekvens x[n] er bundet dersom:

 |x[n]| \leq B_x \leq \infty 

En sekvens x[n] er Absolutt summerbar dersom:

 \sum_{n=-\infty}^\infty |x[n]| < \infty 

En sekvens x[n] er Kvadratisk-summerbar dersom energien:

 E_x = \sum_{n=-\infty}^\infty |x[n]|^2 < \infty 

Dette signalet er et energisignal, ikke alle sekvenser er energisignaler. Periodiske er ikke.

Den gjennomsnittlige effekten til en sekvens, er derfinert:

 P_x = \lim_{n\rightarrow\infty} \frac{1}{2N + 1}\sum_{n=-N}^N |x[n]|^2 

Viktige typer sekvenser

Enhetspulsen (Delta-puls)

 \delta[n-k] = 
\begin{cases}
	1 & n=k \\
	0 & n\neq k
\end{cases} $$

Denne du får standardversjonen ved å sette $k=0$.

#### Enhetssteg

$$ u[n-k] = 
\begin{cases}
	1 & n\geq k \\
	0 & n < k
\end{cases}

Denne du får standardversjonen ved å sette k=0.

Sinus

Dersom en sinus-kurve skal være periodisk med en periode N, og siden vi vet at en diskret-tid sinus er periodisk med 2\pi, har vi at:

\begin{aligned}
	\cos(2\pi n) &= \cos(2\pi f (n+N)) \\
	\Rightarrow 2\pi f N &= 2\pi k \\	
	\Rightarrow f &= \frac{k}{N}
\end{aligned}

Kompleks-eksponensial

 x[n] = Ae^{[2\pi f n + \theta]} 

Denne har også en periodisitet på 2\pi, og sekvensen er periodisk dersom f er rasjonell.

Denne er veldig viktig i diskret-tid Fourier representasjon.

Sampling av en sinus-funksjon

Anta vi sampler en analog sinus-funksjon med intervallene nT = \frac{n}{F_S}:

 x_a(t) = A\cos(\Omega t) = A\cos(2\pi F t) 

Da vil den diskrete sekvensen være:

\begin{aligned}
	x[n] 	&= x_a(nT) \\
				&= A\cos\left[2\pi\frac{F}{F_S}n\right] \\
				&= A\cos\left[2\pi f n\right]
\end{aligned}

Der vi har f=\frac{F}{F_S} eller \omega = \Omega T, som er den relative/normaliserte frekvensen (uavhengig av samlingfreksensen).

Fra før vet vi at:

 
\begin{aligned}
	-\frac{1}{2} < &f \leq \frac{1}{2} \\
	-\frac{F_S}{2} < &f \leq \frac{F_S}{2}
\end{aligned}

Dekomponering av signaler

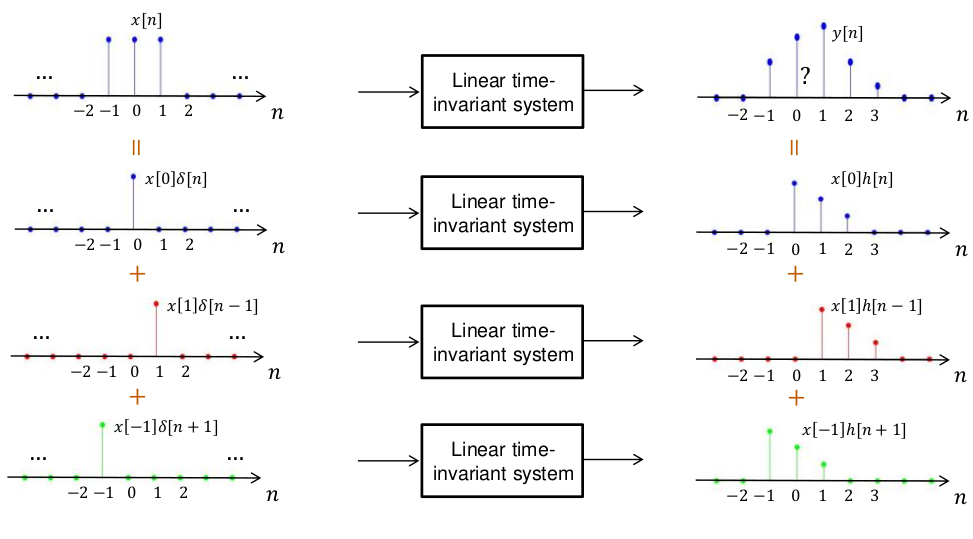
Vi kan få ut en verdi av en sekvens ved å gange inn enhetspulsen på en gitt n.

 x[k] = x[n]\delta[n-k] 

Der hele signalet kan gis som en sum av hver sekvensverdi:

 x[n] = \sum_{k=-\infty}^\infty x[k]\delta[n-k] 

Diskret-tid-systemer

Et diskret-tid-system kan klassifiseres som:

• Lineær eller ikke-lineær
• Tidsinvariant eller tidsvariant
• Kausale eller ikkekausale

I diskret-tid-systemer gjelder følgende:

• Superpossisjon (lineæritet)
• Varierer ikke med tiden (tidsinvariant)
• Kausalt
  • Resultatet er kun avhengig av tidligere eller nåværende verdier
• Ikke-kausalt
  • Gunstig å implimentere der vi vet alle verdier i en sekvens, men ikke i sanntidssystemer.
• Stabile
  • Et system er kun stabilt dersom for hvert bundet inngangssignal er det et bundet utgangssignal.

Impulsrespons

Vi sender ut en enhetspuls og ser på hvordan systemet utvikler seg.

Vi kan finne impulsresponsen ved å sette x[n] = \delta[n]. Da får vi at y[n] = h[n].

Konvulosjon

\begin{aligned}
	y[n] 	&= \mathcal{H}\{x[n]\} \\
				&= \mathcal{H}\left\{\sum_k x[k]\delta[n-k]\right\}\\
				&= \sum_k x[k]\mathcal{H}\left\{\delta[n-k]\right\} \\
				&= \sum_k x[k] h[n-k] \\
				&= x[n] * h[n]
\end{aligned}

Det er mulig å gjøre konvulosjon både stegvis eller med en matrise.

Matrisen er bare å lage en "gangetabell med verdiene i sekvensene, gange sammen og summere anti-diagonalene.

Dersom lengden av sekvensen x[n] er N_x og lengden av h[n] er N_h, vil lengden av konvulosjonen være:

 N_y = N_x + N_h - 1 

Lengde av systemer

Det finnes to typer lengde på impulsresponsen. IIR og FIR.

IIR

"Infinite(-duration) impulse response", er et system der lengden av impulsresponsen er uendelig i lengde. Typisk er utgangen avhengig av forrige resultat.

FIR

"Finite(-duration) impulse response", er et system der impulsresponsen har en endelig lengde.

Diskret-tid Fourieranalyse

Analytisk transformasjon (DTFT)

 X(\omega) = \sum_{n=-\infty}^\infty x[n]e^{-j\omega n} 

Og invers transformasjon (syntetisk transformasjon)

 x[n] = \frac{1}{2\pi}\int_{-\pi}^\pi X(\omega) e^{j\omega n} d\omega

Grensene for frekvensdomenet er fra -\pi til \pi.

Notasjonen er som følger

 x[n] \stackrel{\mathcal{F}}{\leftrightarrow} X(\omega) 

Egenskaper

Symmetri

Odde og like funksjoner, likt som imaginære og ikke imaginære (reelle).

• Odd: x[-n] = -x[n]
• Lik: x[-n] = x[n]

Man kan skrive en sekvens på formen:

 x[n] = \underbrace{x_R[n]}_{\text{reell}} + \underbrace{jx_I[n]}_{\text{imaginær}} 

Andre egenskaper

• Tidsforskyvning

 x[n-k] \stackrel{\mathcal{F}}{\leftrightarrow}e^{-j\omega n}X(\omega) 

• Tidsreversering

 x[-n] \stackrel{\mathcal{F}}{\leftrightarrow} X(-\omega) 

• Konvulosjon

 x_1[n] * x_2[n] \stackrel{\mathcal{F}}{\leftrightarrow} X_1(\omega)X_2(\omega) 

• Frekvensskifting

 e^{j\omega_0 n}x[n] \stackrel{\mathcal{F}}{\leftrightarrow} X(\omega - \omega_0) 

• Modulasjon

 
\begin{gather*}
	x[n] \cos(\omega_0 n) \\
	\updownarrow\mathcal{F} \\
	\frac{1}{2}\left[(X(\omega - \omega_0)+ (X(\omega + \omega_0)\right]
\end{gather*} 

• Parseval

 
\begin{gather*}
	\sum_n |x[n]|^2\\
	\updownarrow\mathcal{F} \\
	\frac{1}{2\pi}\int_{-\pi}^\pi X(\omega)d\omega
\end{gather*} 

• Vindu

 
\begin{gather*}
	x_1[n]x_2[n]\\
	\updownarrow\mathcal{F} \\
	\frac{1}{2\pi}\int_{-\pi}^\pi X_1(\lambda)X_2(\omega - \lambda)d\omega
\end{gather*} 

Z-transformasjon

Z-transformasjonen av et diskret sekvens er gitt som:

 X(z) = \mathcal{Z}\{x[n]\} = \sum_{n=-\infty}^\infty x[n]z^{-n} 

Notasjonen er:

x[n] \stackrel{\mathcal{Z}}{\leftrightarrow} X(z)

x[n] = \mathcal{Z}^{-1}\{X(z)\}

Transformasjonen transformerer en sekvens til den tilsvarende representasjonen i det komplekse z-planet.

ROC (Region of convergence) er settet med alle verdier av z der X(z) har en endelig verdi.

Transformasjonen bestemmer ikke unikt tids-sekvensen. Ved å velge en ROC kan vi lage et ønsket signal/filter.

Dersom vi har at ROC er alt utenfor en sirkel, er sekvensen kausal.

Dersom ROC er innsiden av en sirkel, er sekvensen antikausal.

Egenskaper

• Lineær
  • ROC av resultatet er minst \mathcal{R}\_{X_1} \cap \mathcal{R}\_{X_2}
• Tidsforskyvning
  • ROC lik som for X(z)

 x[n-k] \stackrel{\mathcal{Z}}{\leftrightarrow}z^{-k}X(z) 

• Skalering
  • Dersom ROC før skalering er r_1 < \|z\| < r_2, så er ROC etter lik \|a\|r_1 < \|z\| < \|a\|r_2.

 a^n x[n] \stackrel{\mathcal{Z}}{\leftrightarrow} X(a^{-1} z) 

• Tidsreversering
  • Dersom ROC er r_1 < \|z\| < r_2 , så er ROC etter tidsreversering \frac{1}{r_2} < \|z\| < \frac{1}{r_1}

 x[-n] \stackrel{\mathcal{Z}}{\leftrightarrow} X(z^{-1}) 

• Konvulosjon
  • ROC minst snittet av ROC til X_1 og X_2.

 x_1[n]*x_2[n]\stackrel{\mathcal{Z}}{\leftrightarrow} X_1(z)X_2(z)

• Derivering
  • ROC er den samme
  • Initialverditeroremet: x[0] = \lim_{z\rightarrow \infty}X(z), betyr at x[n] er kausalt.

 nx[n] \stackrel{\mathcal{Z}}{\leftrightarrow} -z\frac{dX(z)}{dz} 

Rasjonelle z-transformasjoner

Rasjonell dersom transformasjonen kan bli representert som forholdet mellom to polynomer i z^{-1} eller z.

\begin{aligned}
	X(z) 	&= \frac{B(z)}{A(z)} \\
				&= \frac{b_0 + b_1 z^{-1} + \ldots + b_M z^{-M} }{a_0 + a_1 z^{-1} + \ldots + a_N z^{-N}} \\
				&= \frac{b_0}{a_0}\frac{\prod_{k=1}^M \left(1-z_k z^{-1}\right)}{\prod_{k=1}^N \left(1-p_k z^{-1}\right)}
\end{aligned}

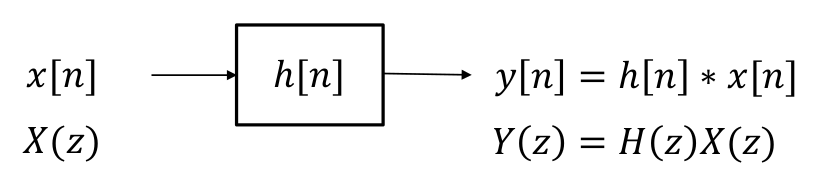
Systemanalyse

Dersom vi har et system som vist over, sender inn en sekvens x[n] eller X(z) og observerer utgangen y[n] eller Y(z), kan vi finne systemfunksjonen.

h[n] = \frac{y[n]}{x[n]}

 H(z) = \frac{Y(z)}{X(z)} 

Vi kan bruke transformasjonen til å gå mellom dem.

Begge er helt ekvivalente.

Kausalitet og stabilitet

For at et system skal være kausalt, må ROC være alt utenfor en sirkel.

For at et system skal være BIBO stabilt, må enhetssirkelen z = e^{-j\omega} være med i ROC.

Det er mulig å bestemme om et system er kausal og stabilt ved å velge ROC.

ROC må heller ikke inneholde noen poler.

Frekvensrespons

For å finne frekvensresponsen til et system, "går" man langs enhetsirkelen, fra -\pi til \pi.

Utregning

Dersom vi har frekvensresponsen til et system:

 H_1(z) = \frac{1}{1-\frac{1}{2}z^{-1}} 

Matlabløsningen er som under

{% highlight matlab %} B = 1; A = [1 -0.5]; figure(1) zplane(B,A) figure(2) [H,W]=freqz(B,A); plot(W/pi,abs(H)); {%endhighlight%}

Filteregenskaper

Frekvensresponsen til et system bestemmer hvordan type system det er.

• Båndpass
  • Slipper gjennom visse frekvenser
• Båndstopp
  • Stopper visse frekvenser
• Lavpass
  • Slipper gjennom lave frekvenser
• Høypass
  • Slipper gjennom høye frekvenser

Lavpass

I et lavpassfilter ønsker vi å putte polene nærme(re) z=1, og nuller nærme(re) z=-1.

Dersom vi ser på et pol-null-plot ser vi at frekvensen er 0 ved z=1, og poler forsterker et signal når vi er "nærme" det (ref tilbake til hvordan finne frevensresponsen til en z-transformasjon).

Høypass

I et høypassfilter ønsker vi det motsatte av et lavpassfilter. Vi ønsker å putte så mange nuller nærheten av z=1, og så mange poler i nærheten av z=-1.

Dette er av samme grunn som for et lavpass.

"Notch"-filter

Kan isolere seg rundt en veldig spesifik frekvens og fjerne den.

For å oppnå dette, så kan man putte noen nuller på enhetssirkelen og noen poler i nærheten av nullene. Da får vi veldig smale bånd.

Kamfilter

Litt som et omvendt "notch"-filter. Det er periodiske nuller langs enhetssirkelen. Ender opp med noe som ligner på en kam.

Allpassfilter

Dette filteret har en amplituderespons på 1. Men den kan endre fasen på signalet ved gitte frekvenser.

Lineær-fase-filtere

Dette er ønskelig, fordi da får vi kun en tidsforsinkning i utgangssignalet i båndpass. For et lavpass er dette for lave frekvenser.

 \angle H(\omega) = a + b\omega 

Der

H(\omega) = |H(\omega)| e^{j\angle H(\omega)} 

Da vil nullene komme i resiproke par. Altså dersom vi har en null i en vinkel, og avstand fra enhetssirkelen. Da vil den resiproke nullen være i samme vinkel, men samme avstand fra enhetssirkelen, bare på andre siden av sirkelen.

Inverse- og minimumsfase-systemer

Dersom et system \mathcal{T} er inverterbart, kan vi finne inngangssignalet dersom vi har utgangsignalet og den inverterbare systemgfunksjonen.

\begin{gather*}
	h[n]*h_I[n] = \delta[n] \\
	\updownarrow\mathcal{Z} \\
	H(z)H_I(z) = 1
\end{gather*}

Minimumsfasefilter

Et system kalles minimumfase dersom alle nuller og poler ligger innenfor enhetssirkelen.

Et stabilt pol-null-system som er av typen minimum fase har en stabil invers som også er minimum fase.

Korrelasjon

Korrelasjon er et mål på likhet.

Krysskorrelasjon

Dersom vi har en sekvens x[n] og y[n], vil kryssrelassjonen mellom disse to være:

 
\begin{aligned}
	r_{xy}[l]	&= \sum_{n=-\infty}^\infty x[n]y[n-l] \\
						&= \sum_{n=-\infty}^\infty x[n + l]y[n] \\
						&\phantom{=} \text{der } l = \pm 1, \pm 2, \ldots
\end{aligned}

Denne måler likheten mellom signalene x[n] og y[n].

Denne er ikke "kommutativ", altså r_{xy}[l] \neq r_{yx}[l].

Men følgende holder:

r_{yx}[l] = r_{xy}[-l]

Autokorrelasjon

Måler selvlikhet, y[n] = x[n].

 
\begin{aligned}
	r_{xx}[l]	&= \sum_{n=-\infty}^\infty x[n]x[n-l] \\
						&= \sum_{n=-\infty}^\infty x[n + l]x[n] \\
						&\phantom{=} \text{der } l = \pm 1, \pm 2, \ldots
\end{aligned}

Egenskaper til autokorrelasjon

Energi i sekvenser x[n]:

 E_x = \sum_{n=-\infty}^\infty x^2[n] = r_{xx}[0] \geq 0 

Autokorrelasjonen har maksimum lag l=0:

 |r_{xx}[l]| \leq r_{xx}[0] = E_x 

Autokorrelasjon er en lik funksjon:

\begin{aligned}
	r_{xy}[l]	&= r_{yx}[-l]	\\
						&\Downarrow		\\
	r_{xx}[l]	&= r_{xx}[-l]
\end{aligned}

Normaliserte versjoner:

\begin{aligned}
	\varrho_{xx}[l]		&= \frac{r_{xx}[l]}{r_{xx}[0]} 	\\
										&\Downarrow 										\\
	|\varrho_{xx}[l]| &\leq 1													\\ \\
	\varrho_{xy}[l]		&= \frac{r_{xy}[l]}{\sqrt{r_{xx}[0]r_{yy}[0]}}\\
										&\Downarrow 																	\\
	|\varrho_{xy}[l]| &\leq 1
\end{aligned}

Spektral tetthet (Energi)

Størrelsen S_{xx}(\omega)\geq 0 er den spektrale tettheten til x[n].

For å finne denne størrelsen, gjør vi en Fourier-transformasjon av autokorrelasjonen r_{xx}[n]:

\begin{aligned}
	r_{xx}[l] 		&= x[l] * x[-l] 					\\
								&\updownarrow \mathcal{F}	\\
	S_{xx}(\omega)&= X(\omega)X^*(\omega)		\\
								&= |X(\omega)|^2
\end{aligned}

Størrelsen S_{xy}(\omega) er den kryssspektrale tettheten.

\begin{aligned}
	r_{xy}[l] 		&= x[l] * y[-l] 					\\
								&\updownarrow \mathcal{F}	\\
	S_{xy}(\omega)&= X(\omega)Y^*(\omega)
\end{aligned}